Bài toán 9.1. Từ điểm M ở ngoài đường tròn (O) kẻ các tiếp tuyến MA, MB với đường tròn. Gọi I là trung điểm của MA và K là giao của BI với đường tròn. Tia MK cắt đường tròn (O) tại C.
a) Chứng minh các tam giác MIK và BIM đồng dạng
b) Chứng minh BC song song với MA.
c) Gọi H là trực tâm của tam giác MAB. Chứng minh rằng khoảng cách HA không phụ thuộc vị trí của M.
d) Xác định vị trí của điểm M để tứ giác AMBC là hình bình hành.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

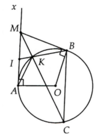
a, ∆IAK:∆IBA => I A I B = I K I A
Mà IA = IM => I M I B = I K I M
=> ∆IKM:∆IMB
b, Chứng minh được: I M K ^ = K C B ^ => BC//MA(đpcm)

a: OH*OM=OA^2=R^2
b: ΔOCD cân tại O
mà OI là đường trung tuyến
nên OI vuông góc với CD
Xét tứ giác OIAM có
góc OIM=góc OAM=90 độ
nên OIAM là tứ giác nội tiếp
c: Xét ΔOHK vuông tại H và ΔOIM vuông tại I có
góc HOK chung
Do đo: ΔOHK đồng dạng với ΔOIM
=>OH/OI=OK/OM
=>OI*OK=OH*OM=R^2=OC^2
mà CI vuông góc với OK
nên ΔOCK vuông tại C
=>KC là tiếp tuyến của (O)