Một quả cầu được truyền cho vận tốc đầu 4m/s tại A, chuyển động trên đường nằm ngang AB = 1,5m có hệ số ma sát µ = 0,3. Sau đó đi tiếp trên đoạn cong BC ma sát không đáng kể (hình vẽ). Tính độ cao h t...

BN

Bách Nguyễn Chí

21 tháng 3 2023

Một quả cầu được truyền cho vận tốc đầu 4m/s tại A, chuyển động trên đường nằm ngang AB = 1,5m có hệ số ma sát µ = 0,3. Sau đó đi tiếp trên đoạn cong BC ma sát không đáng kể (hình vẽ). Tính độ cao h tối đa mà quả cầu lên được tại C. (Cho g = 10m/s²...

Đọc tiếp

#Vật lý lớp 10

0

HD

Hoàng Đức Long

18 tháng 6 2017

Một xe có khối lượng 2 tấn chuyển động trên đoạn AB nằm ngang với vận tốc không đổi 7,2km/h. Hệ số ma sát giữa xe và mặt đường là μ = 0 , 2 , lấy g = 10m/s2.a. Tính lực kéo của động cơ.b. Đến điểm B thì xe tắt máy và xuống dốc BC nghiêng góc 30o so với phương ngang, bỏ qua ma sát. Biết vận tốc tại chân C là 72km/h. Tìm chiều dài dốc BC.c. Tại C xe tiếp tục chuyển...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

18 tháng 6 2017

a. Vì Xe chuyển động thẳng đều nên

F = f m s = μ N = μ m g = 0 , 2.2000.10 = 4000 ( N )

b. v C = 72 ( k m / h ) = 20 ( m / s )

Áp dụng định lý động năng

A = W d C − W d B

Công của trọng lực

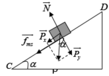
A P = P x . B C = P sin α . B C = m g sin α . B C A P = 2000.10. 1 2 . B C = 10 4 . B C ( J )

⇒ 10 4 . B C = 1 2 . m . v C 2 − 1 2 m . v B 2 ⇒ 10 4 . B C = 1 2 .2000.20 2 − 1 2 .2000.2 2 ⇒ B C = 39 , 6 ( m )

c. Áp dụng định lý động năng

A = W d D − W d C ⇒ A f → m s = 1 2 m v D 2 − 1 2 m v C 2

Công của lực ma sát

A f m s = − f m s . s = − μ N . s = − μ . m g . s / = − μ .2000.10.200 = − μ .4.10 6 ( J )

Dừng lại

v D = 0 ( m / s ) ⇒ − μ 4.10 6 = 0 − 1 2 .2000.20 2 ⇒ μ = 0 , 1

Đúng(0)

HD

Hoàng Đức Long

1 tháng 3 2018

Một vật khối lượng 2kg đặt trên mặt phẳng nằm ngang.Khi tác dụng một lực có độ lớn là 1N theo phương ngang vật bắt đầu trượt trên mặt phẳng nằm nganga. Tính vận tốc của vật sau 4s. Xem lực ma sát là không đáng kể.b. Thật ra, sau khi đi được 8m kể từ lúc đứng yên, vật dạt được vận tốc 2m/s. Tính gia tốc chuyển động, lực ma sát và hệ số ma sát. Lấy g = 10 ...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

1 tháng 3 2018

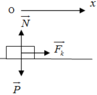
a. Chọn chiều dương là chiều chuyển động.

Theo định luật II Newton P → + N → + F → = m a →

Chiếu lên ox ta có F = m a ⇒ a = F m = 1 2 = 0 , 5 m / s 2

Mà v = v 0 + a t = 0 + 0 , 5.4 = 2 m / s

Áp dụng công thức v 2 − v 0 2 = 2 a s ⇒ a = 2 2 − 0 2 2.8 = 0 , 25 m / s 2

Khi có lực ma sát ta có

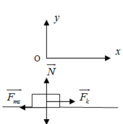
Chọn hệ quy chiếu Oxy như hình vẽ , chiều dương (+) Ox là chiều chuyển động .Áp dụng định luật II Newton. Ta có F → + F → m s + N → + P → = m a →

Chiếu lên trục Ox: F − F m s = m a 1

Chiếu lên trục Oy: N − P = 0 ⇒ N = P

⇒ F − μ N = m a ⇒ μ = F − m . a m g

⇒ μ = 1 − 2.0 , 25 2.10 = 0 , 025

Mà F m s = μ . N = 0 , 025.2.10 = 0 , 5 N

Đúng(0)

HD

Hoàng Đức Long

28 tháng 12 2017

Một vật có khối lượng 2kg trượt qua A với vận tốc 2m/s xuống dốc nghiêng AB dài 2m, cao 1m. Biết hệ số ma sát giữa vật và mặt phẳng nghiêng là µ = 1 3 . lấy g = 10ms-2.a. Xác định công của trọng lực, công của lực ma sát thực hiện khi vật chuyển dời từ đỉnh dốc đến chân dốc.b. Xác định vận tốc của vật tại chân dốc B.c. Tại chân dốc B vật tiếp tục chuyển...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

28 tháng 12 2017

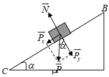
a. Ta có

sin α = 1 2 ; cos α = 3 2

Công của trọng lực

A P = P x . s = P sin α . s = m g sin α . s A P = 2.10. 1 2 .2 = 20 ( J )

Công của lực ma sát

A f m s = − f m s . s = − μ N . s = − μ . m g cos α . s A f m s = − 1 3 .2.10. 3 2 .2 = − 20 ( J )

b. Áp dụng định lý động năng

A = W d B − W d A ⇒ A P → + A f → m s = 1 2 m v B 2 − 1 2 m v A 2 ⇒ 20 − 20 = 1 2 .2 v B 2 − 1 2 .2.2 2 ⇒ v B = 2 ( m / s )

c. Áp dụng định lý động năng

A = W d C − W d B ⇒ A f → m s = 1 2 m v C 2 − 1 2 m v B 2

Công của lực ma sát

A f m s = − f m s . s = − μ N . s = − μ . m g . s / = − μ .2.10.2 = − μ 40 ( J )

Dừng lại

v C = 0 ( m / s ) ⇒ − μ 40 = 0 − 1 2 .2.2 2 ⇒ μ = 0 , 1

Đúng(0)

HD

Hoàng Đức Long

23 tháng 4 2018

Một vật trượt không vận tốc đầu xuống mặt phẳng nghiêng AB rồi tiếp tục đi thêm một đoạn BC trên mặt phẳng ngang. Biết AH = 1 m, BH = 2 m, hệ số ma sát trên cả hai đoạn đường là µ = 0,2. Tính độ dài BC. A. 3 m/s B. 5 m/s C. 2 m/s D. 10...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

23 tháng 4 2018

Đúng(0)

HD

Hoàng Đức Long

26 tháng 4 2017

Một vật đang chuyển động với vận tốc ban đầu v 0 = 8 m / s thì lên dốc cao 0,8m rồi tiếp tục chạy trên mặt phẳng ngang như hình vẽ, mặt phẳng ngang có hệ số ma sát là 0,6. Lấy g = 10 m / s 2 , hỏi nó chuyển động được bao xa trên mặt phẳng ngang thì dừng, coi chiều dài dốc không đáng kể so với quãng đường nó chuyển động được ở...

Đọc tiếp

#Mẫu giáo

1

VT

Vũ Thành Nam

26 tháng 4 2017

Chọn B

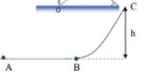
Áp dụng định luật bảo toàn và chuyển hóa cơ năng ở hai vị trí chân dốc và ở vị trí đầu dốc

E 1 − E 0 = μ 1 m g S 1 → S t = 0 1 2 m v 0 2 ⏟ E 0 = 1 2 m v 2 + m g h ⏟ E 1 ⇒ v = v 0 2 − 2 g h

Áp dụng định luật bảo toàn và chuyển hóa cơ năng ở hai vị trí đầu dốc và vị trí vật dừng lại

0 − 1 2 m v 2 = − μ 2 m g . S 2 ⇒ S 2 = v 2 2 μ g = v 0 2 − 2 g h 2 μ g = 4 m

Đúng(0)

HD

Hoàng Đức Long

2 tháng 4 2018

Một ván trượt dài L = 4m, khối lượng phân bố đều theo chiều dài, đang chuyển động với vận tốc v0 = 5m/s trên mặt băng nằm ngang nhẵn ma sát không đáng kể thì gặp một dải đường nhám có ma sát đủ lớn với hệ số ma sát là có chiều rộng l = 2m vuông góc với phương chuyển động (hình bên). Sau khi vượt qua dải nhám vẫn có vận tốc v = 3m/s. Lấy g = 10m/s2. Giá trị của μ bằng A....

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

2 tháng 4 2018

Đáp án B

Cho hệ tọa độ Ox như hình

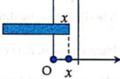
- Khi đầu tấm ván có tọa độ: , lực ma sát tác dụng lên xe có độ lớn:

Đúng(0)

HD

Hoàng Đức Long

24 tháng 4 2017

Người ta đẩy một chiếc họp để truyền cho nó một vận tốc đầu v0 = 3,5m/s. Sau khi đẩy, hộp chuyển động trên sàn nhà. Hệ số ma sát trượt giữa hộp và sàn nhà là µ = 0,3. Hỏi hộp đi được một đoạn đường bằng bao nhiêu ? Lấy g = 9,8m/s2. A. 2,7m B. 3,9m C. 2,1m D....

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

24 tháng 4 2017

Chọn đáp án C

Ta có:

F_ms = µP = µmg

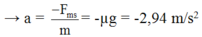
Áp dụng công thức độc lập thời gian có:

v² – v_o² = 2aS

Đúng(0)

HD

Hoàng Đức Long

5 tháng 4 2017

Một ô tô có khối lượng 1 tấn chuyển động trên đường ngang khi qua A có vận tốc 18km/h và đến B cách A một khoảng là 100m với vận tốc 54km/h.a. Tính công mà lực kéo của động cơ đã thực hiện trên đoạn đường AB.b. Đến B tài xế tắt máy và xe tiếp tục xuống dốc nghiêng BC dài 100m, cao 60m. Tính vận tốc tại C.c. Đến C xe vẫn không nổ máy, tiếp tục leo lên dốc nghiêng CD hợp với mặt...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

5 tháng 4 2017

a. Ta có

v A = 18 ( k m / h ) = 5 ( m / s ) ; v B = 54 ( k m / h ) = 15 ( m / s )

Áp dụng định lý động năng

A = 1 2 m v B 2 − 1 2 m v A 2 ⇒ A F → + A f → m s = 1 2 m ( v B 2 − v A 2 )

Mà A f m s = − f m s . s = − μ . N . s = − μ . m . g . s = − 0 , 1.1000.10.100 = − 10 5 ( J ) ⇒ A F → = 1 2 .1000 ( 15 2 − 5 2 ) + 10 5 = 2.10 5 ( J )

b. Ta có

sin α = 60 100 = 3 5 ; cos α = 100 2 − 60 2 100 = 4 5

Áp dụng định lý động năng

A = W d C − W d B ⇒ A P → + A f → m s = 1 2 m v C 2 − 1 2 m v B 2

Công của trọng lực

A P = P x . B C = P sin α . B C = m g sin α . B C A P = 1000.10. 3 5 .100 = 6.10 5 ( J )

Công của lực ma sát

A f m s = − f m s . B C = − μ N . B C = − μ . m g cos α . B C A f m s = − 0 , 1.1000.10. 4 5 .100 = − 8.10 4 ( J )

⇒ 6.10 5 − 8.10 4 = 1 2 .1000. ( v C 2 − 15 2 ) ⇒ v C = 35 , 57 ( m / s )

c. Gọi E là vị trí mà xe có thể lên được

v E = 0 ( m / s )

Áp dụng định lý động năng

A = W d E − W d C ⇒ A P → + A f → m s = − 1 2 m v C 2

Công trọng lực của vật

A P → = − P x . C E = − m g sin 30 0 . C E ⇒ A P → = − 1000.10. 1 2 . C E = − 5000. C E ( J )

Công của lực ma sát

A f m s = − f m s . C E = − μ N . C E = − μ . m . g cos 30 0 . C E = − 500 3 . C E ( J )

⇒ − 5000. C E − 500 3 . C E = − 1 2 .1000. ( 35 , 57 ) 2 ⇒ C E = 107 , 8435 ( m )

Đúng(0)

HD

Hoàng Đức Long

3 tháng 5 2019

Người ta đẩy một chiếc họp để truyền cho nó một vận tốc đầu v 0 = 3 , 5 m / s . Sau khi đẩy, hộp chuyển động trên sàn nhà. Hệ số ma sát trượt giữa hộp và sàn nhà là µ = 0,3. Hỏi hộp đi được một đoạn đường bằng bao nhiêu ? Lấy g = 9 , 8 m / s 2 A. 2,7 m. B. 3,9 m. C. 2,1 m. D. 1,8m...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

3 tháng 5 2019

Đáp án C

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP