Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình: Hai người cùng làm chung công việc hoàn thành trong 4 ngày. Nếu mỗi tổ làm riêng thì thời gian hoàn thành của người thứ hai ít hơn thời gian hoàn thành của người thứ nhất là 6 ngày. Hỏi nếu làm riêng thì mỗi người phải làm trong bao nhiêu ngày để hoàn thành công việc?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
Giả sử người thứ I làm riêng thì sau $a$ giờ thì xong. Khi đó người thứ II làm riêng sau $a+6$ giờ thì xong
Trong 1 giờ:
Người I làm $\frac{1}{a}$ công việc
Người II làm $\frac{1}{a+6}$ công việc
Trong 4 giờ, hai người làm:
$\frac{4}{a}+\frac{4}{a+6}=1$ (công việc)
Với $a>0$ ta dễ dàng tìm được $a=6$ (giờ)
Vậy người I làm riêng mất $6$ giờ, người II làm riêng mất $12$ giờ.
Bài 2:
Thể tích bồn nước là:
$V=S_{đáy}. h=0,42.1,65=0,693(m^3)$
Vậy bồn nước này đựng đầy $0,693$ mét khối nước.

Gọi thời gian hoàn thành công việc khi làm một mình của người 1 và người 2 lần lượt là a,b
Trong 1h,người 1 làm được 1/a(công việc)
Trong 1h, người 2 làm được 1/b(công việc)
Theo đề, ta có:
1/a+1/b=1/(5+5/6) và 5/a+7/b=1
=>1/a+1/b=6/35 và 5/a+7/b=1
=>a=10 và b=14

Gọi thời gian tổ 1 hoàn thành công việc khi làm một mình là x(giờ)
thời gian tổ 2 hoàn thành công việc khi làm một mình là y(giờ)
(Điều kiện: x>12; y>12)
Trong 1 giờ, tổ 1 làm được: \(\dfrac{1}{x}\)(công việc)
Trong 1 giờ, tổ 2 làm được: \(\dfrac{1}{y}\)(công việc)
Trong 1 giờ, hai tổ làm được: \(\dfrac{1}{12}\)(công việc)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\)(1)
Vì khi tổ 1 làm một mình trong 2 giờ và tổ 2 làm một mình trong 7 giờ thi hai tổ làm được một nửa công việc nên ta có phương trình:
\(\dfrac{2}{x}+\dfrac{7}{y}=\dfrac{1}{2}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{2}{x}+\dfrac{7}{y}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{2}{y}=\dfrac{1}{6}\\\dfrac{2}{x}+\dfrac{7}{y}=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-5}{y}=\dfrac{-1}{3}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=15\\\dfrac{1}{x}=\dfrac{1}{12}-\dfrac{1}{15}=\dfrac{1}{60}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=60\\y=15\end{matrix}\right.\)(thỏa ĐK)
Vậy: Tổ 1 cần 60 giờ để hoàn thành công việc khi làm một mình
Tổ 2 cần 15 giờ để hoàn thành công việc khi làm một mình

Gọi x (giờ) là thời gian DCSX 1 làm riêng để xong công việc
y (giờ) là thời gian DCSX 2 làm riêng để xong công việc
Điều kiện : x,y > 12
Trong một giờ, DCSX 1 làm được là : 1/x (công việc)
Trong một giờ, DCSX 2 làm được là : 1/y (công việc)
Vì cả 2 DCSX của nhà máy làm chung đã hoàn thành công việc sau 12h nên ta có phương trình :
1/x + 1/y = 1/12 (1)
Vì nếu làm riêng thì DCSX 1 làm chậm hơn DCSX 2 là 7h để xong công việc nên ta có phương trình :
y - x = 7 (2)
Từ (1) và (2) ta có hệ phương trình : \(\hept{\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac{1}{12}\\y-x=7\end{cases}}\)\(\Leftrightarrow\) \(\hept{\begin{cases}\frac{1}{x}+\frac{1}{x+7}=\frac{1}{12}\\y=x+7\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}\frac{x+7}{x\left(x+7\right)}+\frac{x}{x\left(x+7\right)}=\frac{1}{12}\\y=x+7\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}\frac{2x+7}{x^2+7x}=\frac{1}{12}\\y=x+7\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}12\left(2x+7\right)=x^2+7x\\y=x+7\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}24x+84=x^2+7x\\y=x+7\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}x^2+7x-24x-84=0\\y=x+7\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}x^2-17x-84=0\\y=x+7\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}\orbr{\begin{cases}x_1=21\left(nh\text{ậ}n\right)\\x_2=-4\left(l\text{oại}\right)\end{cases}}\\y=21+7=28\end{cases}}\)\(\hept{\begin{cases}x=21\\y=28\end{cases}}\left(tm\right)\)
Vậy DCSX 1 làm riêng thì sau 21h sẽ xong công việc
DCSX 2 làm riêng thì sau 28h sẽ xong công việc

Gọi thời gian người thứ nhất hoàn thành công việc khi làm một mình là x(h)
Thời gian người thứ hai hoàn thành công việc khi làm một mình là y(h)
Trong 1 giờ, người thứ nhất làm được: \(\dfrac{1}{x}\)(công việc)
Trong 1 giờ, người thứ hai làm được: \(\dfrac{1}{y}\)(công việc)
Trong 1 giờ, hai người làm được: \(\dfrac{1}{4}\)(công việc)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\)(1)
Vì nếu làm 1 mình thì người thứ nhất làm xong việc nhanh gấp đôi người thứ hai nên ta có phương trình: y=2x(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\\2x=y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{2x}=\dfrac{1}{4}\\y=2x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2+1}{2x}=\dfrac{1}{4}\\y=2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=12\\y=2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=12\end{matrix}\right.\)

\(\left(x+1\right)^2+\left(\frac{x+1}{x+2}\right)^2=8\)
\(\left(x+1\right)^2+\frac{\left(x+1\right)^2}{\left(x+2\right)^2}=8\)
\(\left(x+1\right)^2\left(x+2\right)^2+\left(x+1\right)^2=8\left(x+2\right)^2\)
\(x^4+6x^3+6x^2-18x-27=0\)
\(\left(x+3\right)\left(x^2-3\right)\left(x+3\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=-3\\x^2=3\end{cases};x=-3\Rightarrow\orbr{\begin{cases}x=-3\\x=\pm\sqrt{3}\end{cases}}}\)
e thử cách khác :
\(\left(x+1\right)^2+\left(\frac{x+1}{x+2}\right)^2=8\)
\(x^2+2x+1+\frac{\left(x+1\right)^2}{\left(x+2\right)^2}=8\)
\(x^2+2x+1+\frac{x+1}{x+2}=8\)
\(x^2+2x+1\left(x+1\right):\left(x+2\right)=8\)
\(x^2+2x+x+1.\frac{1}{x+2}=8\)
\(x^2+3x+\frac{1}{x+2}=8\)
\(x^3+5x^2-2x-15=0\)
sai rồi :((

Gọi x,y(h) lần lượt thời gian làm riêng xong cv của người 1 và 2(x,y>0)
Trong 1h người 1 làm được 1/x công việc
Trong 1h người 2 làm được 1/y công việc
Trong 1h 2 người làm chung được 1/16 công việc
Ta có pt1: 1/x + 1/y = 1/16
Trong 3h người 1 làm được 3/x công việc
Trong 6h người 2 làm được 6/y công việc
Ta có pt2: 3/x + 6/y =1/4
DONE
Hệ bạn tự giải nha

Để hoàn thành 1 công việc, 2 tổ làm chung trong vòng 6h
--> Trong 1 giờ, 2 tổ làm chung được 1/6 công việc.
--> Sau 2h làm chung, số phần công việc đã hoàn thành là 2/6 công việc-->Số công việc còn lại là 1 - 2/6 =2/3 công việc
Để làm xong 2/3 công việc còn lại, tổ 1 đã mất 10h, vậy số phần công việc mà tổ 1 làm độc lập trong 1 giờ là: 2/3 : 10 =1/15 công việc--> Nếu làm riêng thì tổ 1 sẽ mất 15h để hoàn thảnh cả công việc.
Trong 1 h, 2 tổ làm chung được 1/6 công việc nhưng trong 1/6 công việc làm được đó tổ 1 đã làm 1/15 công việc--> Nếu làm độc lập thì trong 1 h tổ 2 sẽ hoàn thành: 1/6 - 1/15 = 1/10 công việc
--> Nếu làm riêng thì tổ 2 sẽ mất 10 h để hoàn thành cả công việc.

đổi 2 giờ 40 phút=\(\dfrac{8}{3}\) giờ
gọi thời gian đội 1 và đội 2 làm riêng để hoàn thành công việc lần lượt là
x,y(x,y>\(\dfrac{8}{3}\) )
=>hệ pt: \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{\dfrac{8}{3}}=\dfrac{3}{8}\\y-x=4\end{matrix}\right.\) giải hệ pt trên ta được \(\left\{{}\begin{matrix}x=4\left(TM\right)\\y=8\left(TM\right)\end{matrix}\right.\)
vậy nếu làm riêng để hoàn thành công việc thì đội thứ nhất hết 4 giờ
đội thứ 2 hết 8 giờ

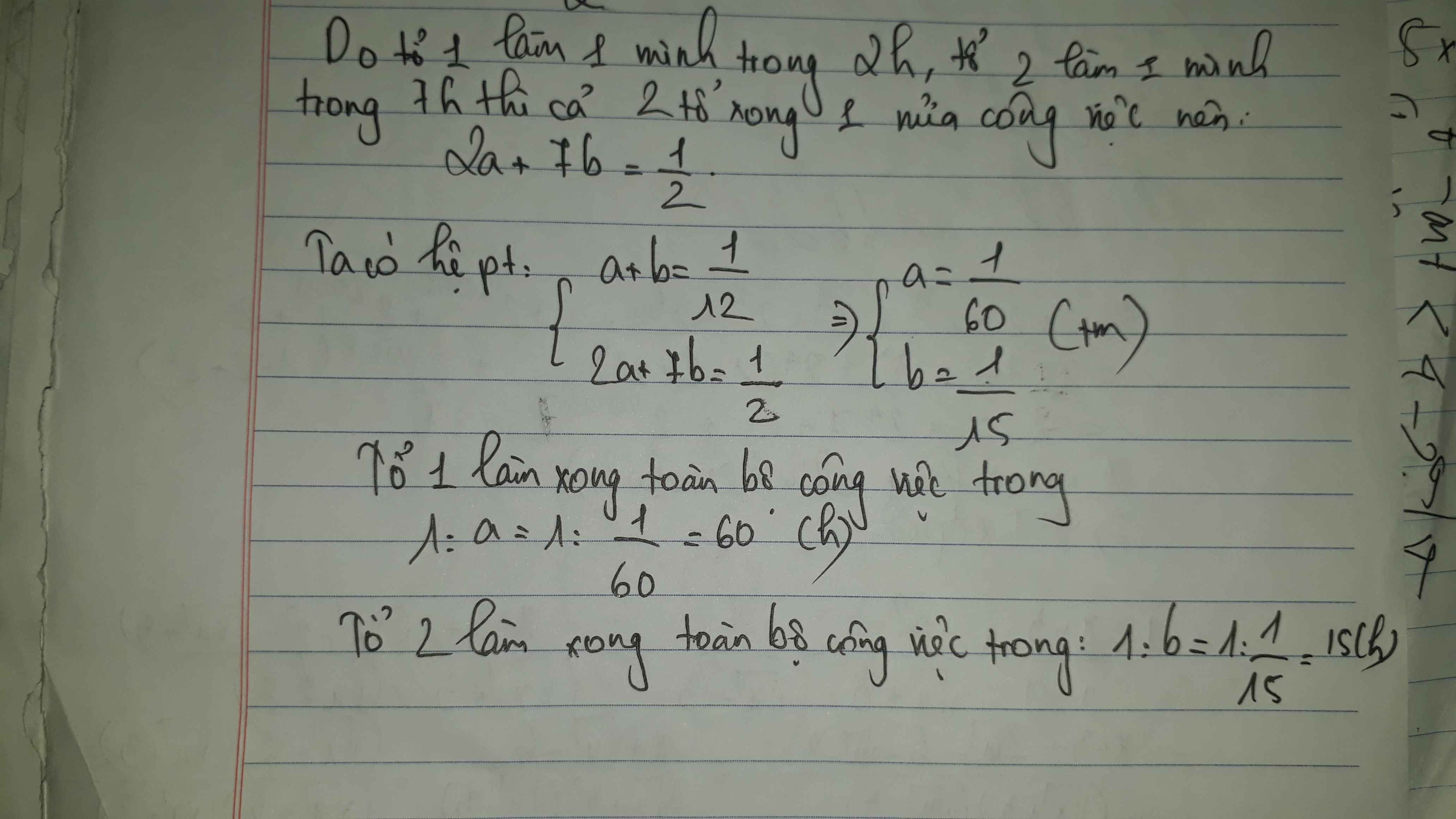
Gọi thời gian làm riêng hoàn thành công việc của người thứ nhất là x (ngày) với x>0
Thời gian làm riêng hoàn thành của hai là y ngày (y>0)
Do người 2 làm ít hơn người 1 là 6 ngày nên: \(x-y=6\)
Trong 1 ngày người thứ nhất làm được \(\dfrac{1}{x}\) phần công việc
Trong 1 ngày người thứ hai làm được \(\dfrac{1}{y}\) phần công việc
Do 2 người làm chung trong 4 ngày xong việc nên: \(4\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=1\)
Ta có hệ: \(\left\{{}\begin{matrix}x-y=6\\\dfrac{4}{x}+\dfrac{4}{y}=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=y+6\\\dfrac{4}{y+6}+\dfrac{4}{y}=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=y+6\\4y+4\left(y+6\right)=y\left(y+6\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=y+6\\y^2-2y-24=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=12\\y=6\end{matrix}\right.\)