Lấy 4 điểm ở miền trong của của tứ giác để cùng với 4 đỉnh của tứ giác đó ta được 8 điểm, trong đó không có ba điểm thẳng hàng. Biết diện tích tứ giác bằng. CMR: tồn tại 1 tam giác có 3 đỉnh lấy từ 8 điểm đã cho có diện tích không vượt quá \(\dfrac{1}{10}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 10 2017
Chọn D
Cách 1:
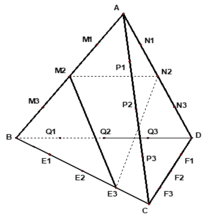
Gọi các điểm được đánh dấu để chia đều các cạnh của tứ diện đều ABCD như hình vẽ.
+ Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu.
Số phần tử của S là số cách chọn ra 3 điểm không thẳng hàng trong số 18 điểm đã cho.
Chọn ra 3 điểm trong 18 điểm trên: có C 18 3 cách.
Chọn ra 3 điểm thẳng hàng trong 18 điểm trên có 6. C 6 3 = 6 cách.
Suy ra số tam giác thỏa mãn là C 18 3 - 6 = 810
+ Gọi T là tập hợp các tam giác lấy từ ABCD sao cho mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện ABCD.
- Chọn 1 cạnh của tứ diện để mặt phẳng chứa tam giác chỉ song song với đúng cạnh đó: có C 6 1 cách.
Xét các tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD, suy ra tam giác đó phải có một cạnh song song với BD.
- Có 6 cách chọn cạnh song song với BD là
- Giả sử ta chọn cạnh M 2 N 2 là cạnh của tam giác. Cần chọn đỉnh thứ 3 của tam giác trong 16 điểm còn lại.
Do M 2 N 2 ⊂ (ABD) mà mặt phẳng chứa tam giác song song với BD nên đỉnh thứ 3 không thể là 7 điểm còn lại nằm trong mp(ABD).
Do mặt phẳng chứa tam giác chỉ song song với BD nên đỉnh thứ 3 không được trùng với một trong ba điểm E 2 , F 2 , P 2 . Vậy đỉnh thứ 3 chỉ được chọn trong 16 -7 - 3 = 6 điểm còn lại.
Suy ra có 6 tam giác có 1 cạnh là M 2 N 2 và mặt phẳng chứa nó chỉ song song với BD.
Vậy số tam giác mà mặt phẳng chứa nó chỉ song song với cạnh BD là: 6.6 = 36.
Tương tự cho các trường hợp khác, ta có số tam giác mà mặt phẳng chứa nó chỉ song song với đúng một cạnh của tứ diện ABCD là: 36.6 = 216.
Vậy xác suất cần tìm là
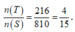
Cách 2: Lưu Thêm
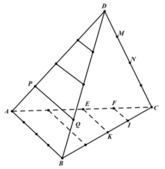
+) Gọi S là tập hợp các tam giác có ba đỉnh lấy từ 18 điểm đã đánh dấu.
Chọn ra 3 điểm trong 18 điểm trên: có C 18 3 cách.
Trong số C 18 3 đó, có 6 cách chọn ra 3 điểm thẳng hàng trên các cạnh.
Suy ra n(S) = C 18 3 - 6 = 810
+) Xét phép thử: “Lấy ngẫu nhiên một phần thử thuộc S”. Ta có 
+) Gọi T là biến cố: “Mặt phẳng chứa tam giác được chọn song song với đúng một cạnh của tứ diện đã cho”.
Chọn một cạnh của tứ diện: 6 cách, (giả sử chọn AB).
Chọn đường thẳng song song với AB: 6 cách, (giả sử chọn PQ).
Chọn đỉnh thứ 3: 6 cách, (M, N, E, K, F, I).
Suy ra n(T) = 6.6.6 = 216
Vậy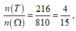 
KN
25 tháng 2 2019
Giải
Xét tứ giác ABCD có AB cắt CD tại F. E là giao điểm 2 đường chéo tứ giác. G,H thứ tự là trung điểm AC,BD
Ta cần chứng minh: \(S_{FGH}=\frac{1}{2}S_{ABCD}\)
\(S_{FGH}=S_{FAD}-S_{FAG}-S_{FDH}-S_{AGD}-S_{DGH}\)
\(=S_{AFD}-\frac{1}{2}\left(S_{FAC}+S_{FBD}\right)-\frac{1}{2}S_{ACD}-\frac{1}{2}S_{DGB}\)
\(=S_{ACD}+S_{ABC}+S_{FBC}-\frac{1}{2}\left(S_{ABC}+S_{FBC}+S_{DBC}+S_{FBC}\right)-\frac{1}{2}S_{ACD}\)
\(-\frac{1}{2}\left(S_{ACD}+S_{ABC}-S_{ADG}-S_{ABG}-S_{DBC}\right)\)
\(=\frac{1}{2}\left(S_{ADG}+S_{ABG}\right)=\frac{1}{2}.\frac{1}{2}\left(S_{ACD}+S_{ABC}\right)=\frac{1}{4}S_{ABCD}\left(đpcm\right)\)
1
27 tháng 2 2019
Giải
Xét tứ giác ABCD có AB cắt CD tại F. E là giao điểm 2 đường chéo tứ giác. G,H thứ tự là trung điểm AC,BD
Ta cần chứng minh: SFGH=12 SABCD
SFGH=SFAD−SFAG−SFDH−SAGD−SDGH
=SAFD−12 (SFAC+SFBD)−12 SACD−12 SDGB
=SACD+SABC+SFBC−12 (SABC+SFBC+SDBC+SFBC)−12 SACD
−12 (SACD+SABC−SADG−SABG−SDBC)
=12 (SADG+SABG)=12 .12 (SACD+SABC)=14 SABCD(đpcm)