Giải hộ em câu này ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HL
1
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 11 2021
1.1
Pt có 2 nghiệm trái dấu và tổng 2 nghiệm bằng -3 khi:
\(\left\{{}\begin{matrix}ac< 0\\x_1+x_2=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\left(m+2\right)< 0\\\dfrac{2m+1}{m+2}=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -2\\m=-\dfrac{7}{5}\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn
b.
Pt có nghiệm kép khi:
\(\left\{{}\begin{matrix}m+2\ne0\\\Delta=\left(2m+1\right)^2-8\left(m+2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-2\\4m^2-4m-15=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=\dfrac{5}{2}\\m=-\dfrac{3}{2}\end{matrix}\right.\)
12 tháng 12 2021
a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp
TA
11 tháng 8 2021
B, Đồ thị y thì nhìn vào dáng điệu, đồ thị y' thì chú ý trục hoành
A
2
20 tháng 1 2022
a: \(\text{Δ}=1-4m\)
Để phương trình vô nghiệm thì -4m+1<0
=>m>1/4
Để phương trình có nghiệm kép thì -4m+1=0
hay m=1/4
Để phương trình có vô số nghiệm thì -4m+1>0
hay m<1/4
b: \(\text{Δ}=9-4\cdot1\cdot\left(-m\right)=4m+9\)
Để phương trình vô nghiệm thì 4m+9<0
hay m<-9/4
Để phương trình có nghiệm kép thì 4m+9=0
hay m=-9/4
Để phương trình có 2 nghiệm phân biệt thì 4m+9>0
hay m>-9/4
T
1
A
1
12 tháng 12 2021
\(b,\Leftrightarrow\left\{{}\begin{matrix}m+2=1\\m\ne2\end{matrix}\right.\Leftrightarrow m=-1\\ c,\text{PT giao Ox: }y=0\Leftrightarrow\left(m+2\right)x-m=0\\ \text{Thay }x=2\Leftrightarrow2m+4-m=0\\ \Leftrightarrow m=-4\\ d,\text{PT giao Ox và Oy: }\\ y=0\Leftrightarrow x=\dfrac{m}{m+2}\Leftrightarrow A\left(\dfrac{m}{m+2};0\right)\Leftrightarrow OA=\left|\dfrac{m}{m+2}\right|\\ x=0\Leftrightarrow y=-m\Leftrightarrow B\left(0;-m\right)\Leftrightarrow OB=\left|m\right|\\ \Delta OAB\text{ cân }\Leftrightarrow OA=OB\Leftrightarrow\left|\dfrac{m}{m+2}\right|=\left|m\right|\\ \Leftrightarrow\left[{}\begin{matrix}\dfrac{m}{m+2}=m\\\dfrac{m}{m+2}=-m\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m\left(m+1\right)=0\\m\left(m+3\right)=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=0\\m=-1\\m=-3\end{matrix}\right.\)
NB
1
28 tháng 8 2021
a: Ta có: \(x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
d: Ta có: \(x^2-2x+\left|y+1\right|+5\)
\(=\left(x-1\right)^2+\left|y+1\right|+4\ge4\forall x,y\)
Dấu '=' xảy ra khi x=1 và y=-1
TL
0
2 tháng 2 2023
Bạn ko đưa ngữ liệu, đưa ngang như v ai hiểu gì đâu
Bạn học sách mới mà.
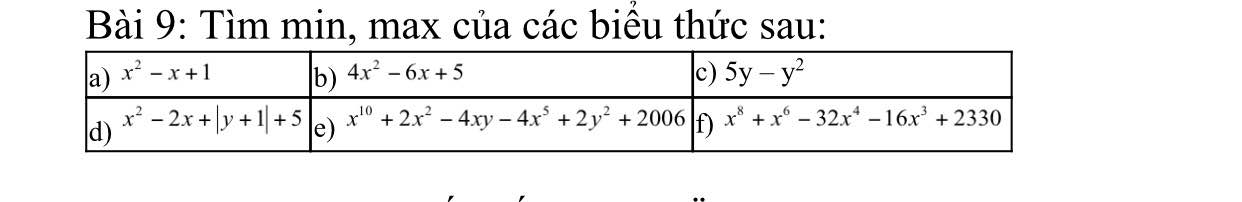
a.
$C=\frac{n+1}{n-2}=\frac{(n-2)+3}{n-2}=1+\frac{3}{n-2}$
Để $C$ nguyên thì $\frac{3}{n-2}$ nguyên. Với $n$ nguyên thì điều này xảy ra khi $n-2$ là ước của $3$
$\Rightarrow n-2\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{3; 1; -1; 5\right\}$
b. Để $D$ có giá trị nguyên thì:
$2n+1\vdots 5n-3$
$\Rightarrow 5(2n+1)\vdots 5n-3$
$\Rightarrow 10n+5\vdots 5n-3$
$\Rightarrow 2(5n-3)+11\vdots 5n-3$
$\Rightarrow 11\vdots 5n-3$
$\Rightarrow 5n-3\in\left\{\pm 1; \pm 11\right\}$
$\Rightarrow n\in\left\{\frac{2}{5}; \frac{4}{5}; \frac{14}{5}; \frac{-8}{5}\right\}$
Vì các số trên không số nào nguyên nên không tồn tại $n$ thỏa mãn.