 giải hộ mình zới
giải hộ mình zới
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




b: Xét ΔAHC vuông tại H có
\(AH^2+HC^2=AC^2\)
nên \(AC^2-HC^2=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AH^2=AN\cdot AC\left(2\right)\)
Từ (1) và (2) suy ra \(AN\cdot AC=AC^2-HC^2\)


\(a,A=\dfrac{9x}{x}:\left[\dfrac{x\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)^2}-\dfrac{4\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}\right]\\ A=9:\left(\dfrac{x}{\sqrt{x}-2}-\dfrac{4}{\sqrt{x}-2}\right)=9:\dfrac{x-4}{\sqrt{x}-2}\\ A=\dfrac{9\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{9}{\sqrt{x}+2}\\ b,x=11+2\sqrt{30}\Leftrightarrow\sqrt{x}=\sqrt{6}+\sqrt{5}\\ \Leftrightarrow A=\dfrac{9}{\sqrt{6}+\sqrt{5}+2}=\dfrac{9\left(\sqrt{6}+\sqrt{5}-2\right)}{7+2\sqrt{30}}\\ \Leftrightarrow A=\dfrac{9\left(\sqrt{6}+\sqrt{5}-2\right)\left(2\sqrt{30}-7\right)}{71}\)
\(c,A+\sqrt{x}=\dfrac{9}{\sqrt{x}+2}+\sqrt{x}=\dfrac{9}{\sqrt{x}+2}+\left(\sqrt{x}+2\right)-2\\ A+\sqrt{x}\ge2\sqrt{\dfrac{9\left(\sqrt{x}+2\right)}{\sqrt{x}+2}}-2=2\sqrt{9}-2=4\left(đpcm\right)\)

c: Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{NAM}=90^0\)
Do đó: AMHN là hình chữ nhật
Suy ra: AH=MN

a: \(x+\dfrac{3}{7}=\dfrac{2}{5}+\dfrac{3}{10}=\dfrac{4}{10}+\dfrac{3}{10}=\dfrac{7}{10}\)
\(\Leftrightarrow x=\dfrac{7}{10}-\dfrac{3}{7}=\dfrac{49}{70}-\dfrac{30}{70}=\dfrac{19}{70}\)
b: \(\dfrac{19}{20}-x=\dfrac{8}{5}-\dfrac{3}{4}=\dfrac{32}{20}-\dfrac{15}{20}=\dfrac{17}{20}\)
=>x=19/20-17/20=2/20=1/10
c: \(\dfrac{7}{5}-x\cdot\dfrac{1}{4}=\dfrac{13}{20}\)
\(\Leftrightarrow x\cdot\dfrac{1}{4}=\dfrac{7}{5}-\dfrac{13}{20}=\dfrac{28}{20}-\dfrac{13}{20}=\dfrac{7}{20}\)
=>x=7/5





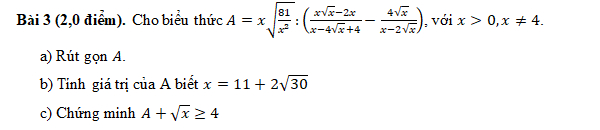

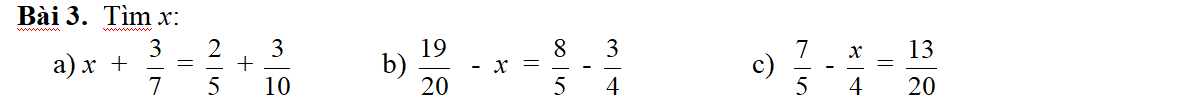
9:
a: Gọi ƯCLN(4n+8;2n+3)=d
=>4n+8-4n-6 chia hết cho d
=>2 chia hết cho d
mà 2n+3 lẻ
nên d=1
=>PSTG
b: Gọi d=ƯCLN(4n+5;5n+6)
=>20n+25-20n-24 chia hết cho d
=>1 chia hêt cho d
=>d=1
=>PSTG
giải luôn giùm mình bài 10 nha !cảm ơn bạn