\(\dfrac{16}{17}:^{1\dfrac{1}{17}}:^{1\dfrac{1}{18}}:^{1\dfrac{1}{19}}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 1 2023
\(A=\dfrac{19+\dfrac{18}{2}+\dfrac{17}{3}+\dfrac{16}{4}+...+\dfrac{1}{19}}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{20}}\)
Biến đổi tử số
\(19+\dfrac{18}{2}+\dfrac{17}{3}+\dfrac{16}{4}+...+\dfrac{1}{19}\)
= 1 + \(\left(1+\dfrac{18}{2}\right)+\left(1+\dfrac{17}{3}\right)+\left(1+\dfrac{16}{4}\right)+...+\left(1+\dfrac{1}{19}\right)\)
= \(\dfrac{20}{20}+\dfrac{20}{2}+\dfrac{20}{3}+...+\dfrac{1}{19}\)
= 20 x \(\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{19}+\dfrac{1}{20}\right)\)
Vậy \(A=\dfrac{19+\dfrac{18}{2}+\dfrac{17}{3}+\dfrac{16}{4}+...+\dfrac{1}{19}}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{20}}\)
= \(\dfrac{20\times\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{19}+\dfrac{1}{20}\right)}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{20}}=20\)
Vậy A = 20
12 tháng 3 2023
a: \(17A=\dfrac{17^{19}+17}{17^{19}+1}=1+\dfrac{16}{17^{19}+1}\)
\(17B=\dfrac{17^{18}+17}{17^{18}+1}=1+\dfrac{16}{17^{18}+1}\)
mà 17^19+1>17^18+1
nên A<B
b: \(2C=\dfrac{2^{2021}-2}{2^{2021}-1}=1-\dfrac{1}{2^{2021}-1}\)
\(2D=\dfrac{2^{2022}-2}{2^{2022}-1}=1-\dfrac{1}{2^{2022}-1}\)
2^2021-1<2^2022-1
=>1/2^2021-1>1/2^2022-1
=>-1/2^2021-1<-1/2^2022-1
=>C<D
3 tháng 3 2022
Bài 1:
1: \(17A=\dfrac{17^{19}+17}{17^{19}+1}=1+\dfrac{16}{17^{19}+1}\)
\(17B=\dfrac{17^{18}+17}{17^{18}+1}=1+\dfrac{16}{17^{18}+1}\)
mà \(17^{19}+1>17^{18}+1\)
nên 17A>17B
hay A>B
2: \(C=\dfrac{98^{99}+98^{10}+1-98^{10}}{98^{89}+1}=98^{10}+\dfrac{1-98^{10}}{98^{89}+1}\)
\(D=\dfrac{98^{98}+98^{10}+1-98^{10}}{98^{88}+1}=98^{10}+\dfrac{1-98^{10}}{98^{88}+1}\)
mà \(98^{89}+1>98^{88}+1\)
nên C>D
2 tháng 5 2017
Ta có:\(\dfrac{1}{13}+\dfrac{1}{14}+\dfrac{1}{15}+\dfrac{1}{16}>4\cdot\dfrac{1}{16}=\dfrac{1}{4}\)
\(\dfrac{1}{17}+\dfrac{1}{18}+\dfrac{1}{19}+\dfrac{1}{20}>4\cdot\dfrac{1}{20}=\dfrac{1}{5}\)
=>\(\dfrac{1}{13}+\dfrac{1}{14}+...+\dfrac{1}{20}>\dfrac{1}{4}+\dfrac{1}{5}=\dfrac{9}{20}\)
=>A>\(\dfrac{1}{12}+\dfrac{9}{20}\)
\(\dfrac{1}{12}>\dfrac{1}{20}\)
=>\(A>\dfrac{1}{20}+\dfrac{9}{20}=\dfrac{1}{2}\)
Vậy...
HN
3 tháng 5 2017
Ta có: \(\dfrac{1}{19}+\dfrac{2}{18}+...+\dfrac{19}{1}=\left(\dfrac{1}{19}+1\right)+\left(\dfrac{2}{18}+1\right)+...+1\)
\(=\dfrac{20}{19}+\dfrac{20}{18}+...+\dfrac{20}{2}+\dfrac{20}{20}=20\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{20}\right)\)
Thế lại bài toán ta được
\(\dfrac{\dfrac{1}{19}+\dfrac{2}{18}+...+\dfrac{19}{1}}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{20}}=\dfrac{20\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{20}\right)}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{20}}=20\)
MV
3 tháng 5 2017
Ta có
\(\dfrac{1}{19}+\dfrac{2}{18}+\dfrac{3}{17}+...+\dfrac{19}{1}\\ =\dfrac{1}{19}+1+\dfrac{2}{18}+1+\dfrac{3}{17}+1+...+\dfrac{19}{1}+1-19\\ =\dfrac{20}{19}+\dfrac{20}{18}+\dfrac{20}{17}+...+\dfrac{20}{1}-19\\ =\dfrac{20}{19}+\dfrac{20}{18}+...+\dfrac{20}{2}+20-19\\ =\dfrac{20}{19}+\dfrac{20}{18}+\dfrac{20}{17}+...+\dfrac{20}{2}+1+19-19\\ =\dfrac{20}{20}+\dfrac{20}{19}+\dfrac{20}{18}+...+\dfrac{20}{2}\\ =20\cdot\left(\dfrac{1}{20}+\dfrac{1}{19}+\dfrac{1}{18}+...+\dfrac{1}{2}\right)\)
Thế vào ta có:
\(\dfrac{\dfrac{1}{19}+\dfrac{2}{18}+\dfrac{3}{17}+...+\dfrac{19}{1}}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{20}}\\ =\dfrac{20\cdot\left(\dfrac{1}{20}+\dfrac{1}{19}+\dfrac{1}{18}+...+\dfrac{1}{2}\right)}{\dfrac{1}{20}+\dfrac{1}{19}+\dfrac{1}{18}+...+\dfrac{1}{2}}\\ =20\)
7 tháng 5 2021
Giải:
a) A=1718+1/1719+1
17A=1719+17/1719+1
17A=1719+1+16/1719+1
17A=1+16/1719+1
Tương tự:
B=1717+1/1718+1
17B=1718+17/1718+1
17B=1718+1+16/1718+1
17B=1+16/1718+1
Vì 16/1719+1<16/1718+1 nên 17A<17B
⇒A<B
b) A=108-2/108+2
A=108+2-4/108+2
A=1+-4/108+2
Tương tự:
B=108/108+4
B=108+4-4/108+1
B=1+-4/108+1
Vì -4/108+2>-4/108+1 nên A>B
c)A=2010+1/2010-1
A=2010-1+2/2010-1
A=1+2/2010-1
Tương tự:
B=2010-1/2010-3
B=2010-3+2/2010-3
B=1+2/2010-3
Vì 2/2010-3>2/2010-1 nên B>A
⇒A<B
Chúc bạn học tốt!
12 tháng 3 2023
17A=1719+1+16/1719+1
17A=1+16/1719+1
phần in nghiêng mình không hiểu lắm, bn giải thích cho mình được ko?
22 tháng 7 2021
a) Ta có: \(\dfrac{5}{8}+\dfrac{3}{17}+\dfrac{4}{18}+\dfrac{20}{-17}+\dfrac{-2}{9}+\dfrac{21}{56}\)
\(=\left(\dfrac{3}{17}-\dfrac{20}{17}\right)+\left(\dfrac{2}{9}-\dfrac{2}{9}\right)+\left(\dfrac{5}{8}+\dfrac{3}{8}\right)\)
\(=-1+1=0\)
b) Ta có: \(\left(\dfrac{9}{16}+\dfrac{8}{-27}\right)+\left(1+\dfrac{7}{16}+\dfrac{-19}{27}\right)\)
\(=\left(\dfrac{9}{16}+\dfrac{7}{16}\right)+\left(\dfrac{-8}{27}-\dfrac{19}{27}\right)+1\)
=1-1+1=1
7 tháng 7 2021
Ta có \(\dfrac{6}{15}>\dfrac{6}{16}>...>\dfrac{6}{19}\) nên \(S< \dfrac{6}{15}.5=2\).
Lại có \(S>\dfrac{6}{19}.5>1\) nên \(1< S< 2\)
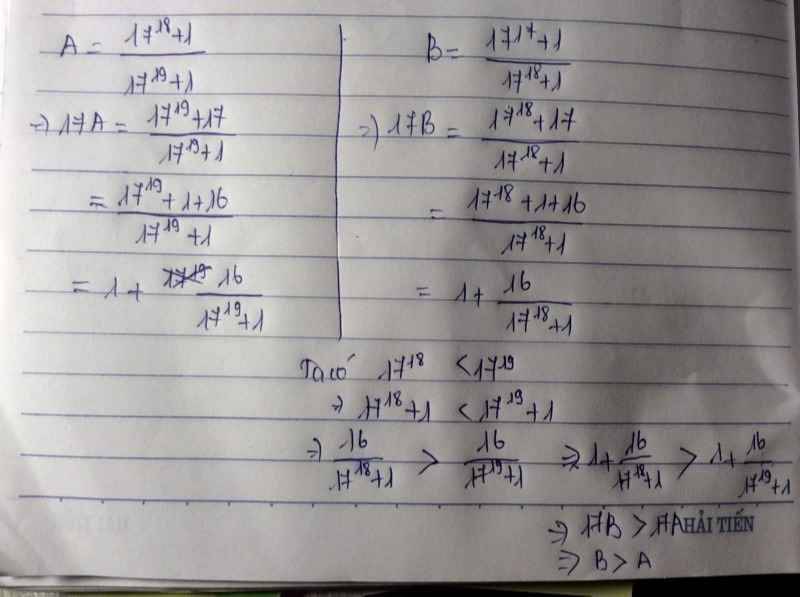
\(\dfrac{16}{17}:1\dfrac{1}{17}:1\dfrac{1}{18}:1\dfrac{1}{19}\)
\(=\dfrac{16}{17}:\dfrac{18}{17}:\dfrac{19}{18}:\dfrac{20}{19}=\dfrac{16}{17}.\dfrac{17}{18}.\dfrac{18}{19}.\dfrac{19}{20}=\dfrac{16}{20}=\dfrac{4}{5}\)