A B C F E D Hãy vẽ điểm H sao cho các bộ ba điểm E,F,H và B,C,H đều là bộ ba điểm thẳng...
Đọc tiếp
Hãy vẽ điểm H sao cho các bộ ba điểm E,F,H và B,C,H đều là bộ ba điểm thẳng hàng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
11 tháng 3 2023
Đúng(0)
Những câu hỏi liên quan
CM
9 tháng 5 2019
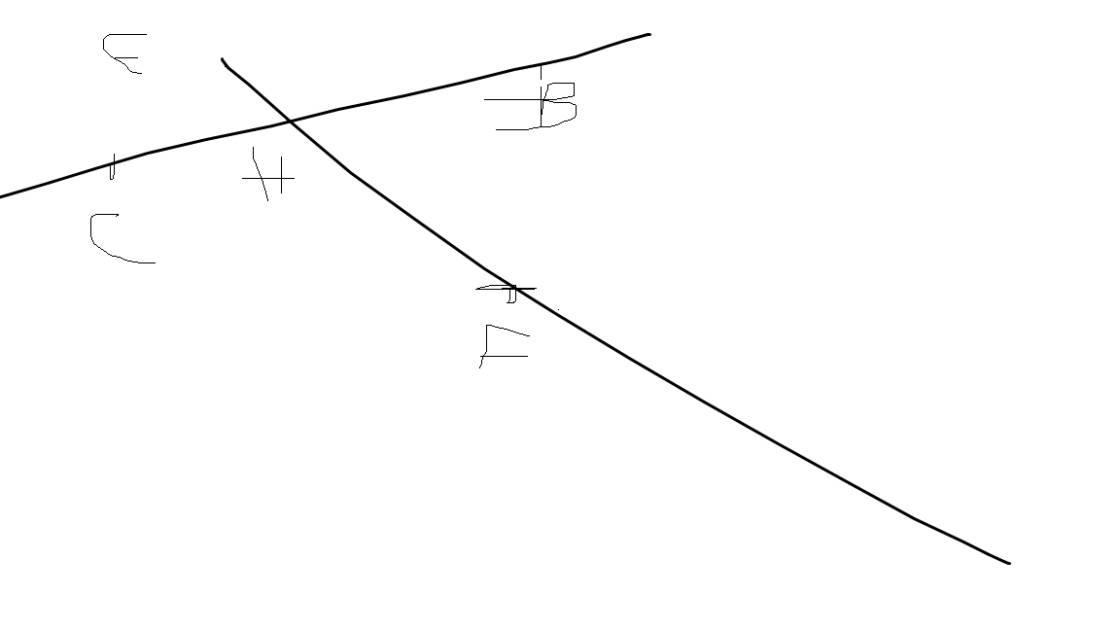
a) Các bộ ba điểm thẳng hàng:
A, F, D A, E, C
B, F, E B, D, C
b) Hai bộ ba điểm không thẳng hàng:
A, F, C A, E, D
c) Điểm F nằm giữa hai điểm A và D.
Điểm F nằm giữa hai điểm B và E.
d) Điểm D nằm giữa hai điểm B và C.
e) Hai điểm B và F nằm cùng phía với điểm E.
f) Hai điểm B và C nằm khác phía với điểm D.
24 tháng 1
Các bộ ba điểm thẳng hàng là A,B,C; A,B,D; B,C,D; A,C,D
Các bộ ba điểm không thẳng hàng là:
A,B,E
B,C,E
C,D,E
A,C,E
A,D,E
B,D,E
HQ
Hà Quang Minh
Giáo viên
8 tháng 10 2023
Bộ ba điểm thẳng hàng: (A, B, C) ; (B, C, D); ( A, C, D); (A, B, D).
Bộ ba điểm không thẳng hàng: (A, B, E); ( A, C, E); ( A, D, E); ( B,C, E), (B, D, E), (C, D, E).
CM
22 tháng 3 2018
a) Chứng minh tứ giác ABOC nội tiếp được đường tròn.
A B O ^ = 90 0 A C O ^ = 90 0 A B O ^ + A C O ^ = 180 0
=> tứ giác ABOC nội tiếp được đường tròn.
b) Vẽ cát tuyến ADE của (O) sao cho ADE nằm giữa 2 tia AO, AB; D, E Î (O) và D nằm giữa A, E. Chứng minh A B 2 = A D . A E .
Tam giác ADB đồng dạng với tam giác ABE
⇒ A B A E = A D A B ⇔ A B 2 = A D . A E
c) Gọi F là điểm đối xứng của D qua AO, H là giao điểm của AO và BC. Chứng minh: ba điểm E, F, H thẳng hàng.
Ta có D H A ^ = E H O ^
nên D H A ^ = E H O ^ = A H F ^ ⇒ A H E ^ + A H F ^ = 180 0 ⇒ 3 điểm E, F, H thẳng hàng.
19 tháng 5 2022
Có 1 phần câu trả lời ở đây.
Giải toán: Bài hình trong đề thi HK2 Lớp 9 | Rất phức tạp. - YouTube