một số sản xuất dự định làm 120 sản phẩm trong thời gian quy định. Trong thực tế mỗi giờ đã làm thêm được 20 sản phẩm. Nên chẳng những đã hoàn thành sớm hơn dự định 1 giờ 30 phút mà còn làm thêm được 5 sản phẩm. Tính năng suất dự định của tổ đó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


gọi x là số sản phẩm được giao ,đk:x>0;
t dự định làm xong:x/20 (x phần 20 nhé)
t thực tế làm xong:x+12/24
Ta có pt: x/20 - x+12/24 = 3
<=> (dấu tương đương) 6x-5x-60=360(MC=120)
<=>x-420=0
=>(dấu suy ra) x=420
vậy số sản phẩm được giao là 420 sản phẩm

dổi 30 phút =1/2 h
gọi x là thời gian người đó định hoàn thành sản phẩm theo dự định ,dơn vị h
gọi y là số sản phẩm ban đầu mà người dó làm dược trong một giờ
=> xy= 150
Do mỗi giờ sản xuất làm nhiều hơn dự định 2 sản phẩm nên tổ không những làm xong trước dự định 30 phút mà còn làm thêm được 4 sản phẩm
=> (x-1/2) (y+2)=54 => xy -1/2y +2x -1 =154
=> 2x -1/2y =154-xy
=>2x-1/2y=4(do xy=150)
=> xy =y(2+1/4y) =2y +1/4 y^2 =150
Rồi,Đến đó bạn tự tính nhé,mk không giải nữa đâu

Đổi 30 phút =1/2 h
Gọi năng suất người công nhân theo kế hoạch là x(sản phâm/h) ĐK: \(x>0,x\in N\)
Theo kế hoạch thì thời gian mà người đó hoàn thành 60sp là \(\frac{60}{x}\left(h\right)\)
Nhưng trên thực tế người công nhân đó mỗi giờ làm thêm 2 sản phẩm vậy năng suất thự tế là \(x+2\)(sp/h)
Số sản phẩm mà người đó làm được trên thực tế là \(60+3=63\left(sp\right)\)
Do đó thời gian thực tế mà người đó hoàn thành công việc là \(\frac{63}{x+2}\left(h\right)\)
Vì kế hoạch được hoàn thành sớm hơn dự định 1/2 h nên ta có pt sau:
\(\frac{60}{x}-\frac{63}{x+2}=\frac{1}{2}\)
\(\Leftrightarrow\frac{60x+120}{x\left(x+2\right)}-\frac{63x}{x\left(x+2\right)}=\frac{1}{2}\)
\(\Leftrightarrow\frac{-3x+120}{x^2+2x}=\frac{1}{2}\)
\(\Leftrightarrow x^2+2x=-6x+240\)
\(\Leftrightarrow x^2+8x-240=0\)
\(\Leftrightarrow x^2-12x+20x-240=0\)
\(\Leftrightarrow x\left(x-12\right)+20\left(x-12\right)=0\)
\(\Leftrightarrow\left(x-12\right)\left(x+20\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=12\left(tm\right)\\x=-20\left(loai\right)\end{cases}}\)
Vậy theo kế hoạch mỗi giờ người đó làm được 12 sản phẩm
Gọi số sản phẩm người đó phải hoàn thành theo kế hoạch trong mỗi giờ là a (sản phẩm) (a>0)
Nên số giờ người đó dự định hoàn thành 60 sản phẩm là \(\frac{60}{a}\) (giờ)
Do cải tiến kĩ thuật nên mỗi giờ người đó làm được a+2 (sản phẩm), và còn vượt mức 3 sản phẩm nên thời gian hoàn thành công việc thực tế là \(\frac{60+3}{a+2}\left(giờ\right)\)
Sớm hơn dự định 30 phút = \(\frac{1}{2}\) giờ, nên ta có:
\(\frac{60}{a}-\frac{60+3}{a+2}=\frac{1}{2}\)
\(\Rightarrow\left[60\left(a+2\right)-63a\right]2=a^2+2a\)
\(\Rightarrow a^2+8a-240=0\)
\(\Delta'=4^2+240=256>0\)
\(\Rightarrow a=-4-\sqrt{256}=-20< 0\left(l\right)\)
Hoặc \(a=-4+\sqrt{256}=12\) ( nhận )
Vậy theo kế hoạch mỗi giờ người đó làm 12 sản phẩm.

Lời giải:
Đổi $1h40'=\frac{5}{3}$ h
Giả sử theo quy định mỗi giờ người đó làm được $a$ sản phẩm $(a>0$), thời gian dự định là $t$ giờ.
Theo bài ra ta có:
$50=at=(a+5)(t-\frac{5}{3})$
\(\Rightarrow \left\{\begin{matrix} 3t-a=5\\ at=50\end{matrix}\right.\Rightarrow t(3t-5)-50=0\)
\(\Rightarrow t=5\) (do $t>0$)
$\Rightarrow a=\frac{50}{t}=10$ (sản phẩm/h)

Gọi số sản phẩm công nhân dự định làm trong một giờ là x (0 < x ≤ 20).
Thời gian dự kiến người đó làm xong 85 sản phẩm là 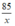 (giờ)
(giờ)
Thực tế mỗi giờ làm tăng thêm 3 sản phẩm nên số sản phẩm làm được mỗi giờ là x + 3.
Do đó 96 sản phẩm được làm trong  (giờ)
(giờ)
Thời gian hoàn thành công việc thực tế sớm hơn so với dự định là 20 phút = 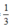 giờ nên ta có phương trình
giờ nên ta có phương trình
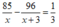
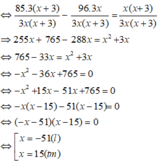
Vậy theo dự định mỗi giờ người đó phải làm 15 sản phẩm.
Chọn đáp án C

Gọi số sản phẩm công nhân làm trong 1 h là x( x<45)
Vì thực tế mỗi giờ sản xuất thêm 1 sp nên số sp làm trong 1 h thực tế là: x+1
Vì hoàn thành sớm hơn dự định 18 phút và còn làm thêm được 2 sản phẩm nên ta có pt:
\(\dfrac{45}{x}-\dfrac{47}{x+1}=\dfrac{3}{10}\)
⇔x=9(TM)
Vậy trong 1h người đó làm được 9 sp theo dự định

Gọi x là số sp dự kiến làm trong 1h của người cn đó. ( 0 < x <= 20)
=> số sp thực tế mà người cn đó làm trong 1h là: x + 1
Thời gian dự kiến để người đó hoàn thành 72 sp là: 72/x ( h)
Thời gian thực tế để người đó hoàn thành 80 sp là: 80/(x+1) (h)
Do thời gian thực tế hoàn thành công việc chậm so với dự kiến 12 phút = 12/60 h = 1/5 h, nên ta có pt sau:
80/(x + 1) - 72/x = 1/5
Giải pt này ta được: x = 34 hoặc x = 15
Vì 0 < x <= 20 => x = 15.
KL: số sp dự kiến làm trong 1h của người cn đó là 15 sp.
Gọi x là số sp dự kiến làm trong 1h của người cn đó. ( 0 < x <= 20)
=> số sp thực tế mà người cn đó làm trong 1h là: x + 1
Thời gian dự kiến để người đó hoàn thành 72 sp là: 72/x ( h)
Thời gian thực tế để người đó hoàn thành 80 sp là: 80/(x+1) (h)
Do thời gian thực tế hoàn thành công việc chậm so với dự kiến 12 phút = 12/60 h = 1/5 h, nên ta có pt sau:
80/(x + 1) - 72/x = 1/5
Giải pt này ta được: x = 34 hoặc x = 15
Vì 0 < x <= 20 => x = 15.
KL: số sp dự kiến làm trong 1h của người cn đó là 15 sp.

Bài 21:
Gọi x (sản phẩm/giờ) là năng suất dự kiến ban đầu của người đó \(\left(x\inℕ^∗\right)\)
=> x + 2 (sản phẩm/giờ) là năng suất lúc sau của người đó
Theo bài ta có phương trình sau:
\(\frac{150}{x}-\frac{1}{2}-2=\frac{150-2x}{x+2}\)
\(\Leftrightarrow300\left(x+2\right)-x\left(x+2\right)-4x\left(x+2\right)=2\left(150-2x\right)x\)
\(\Leftrightarrow300x+600-x^2-2x-4x^2-8x=300x-4x^2\)
\(\Leftrightarrow x^2+10x-600=0\)
\(\Leftrightarrow\left(x-20\right)\left(x+30\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-20=0\\x+30=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=20\left(tm\right)\\x=-30\left(ktm\right)\end{cases}}\)
Vậy ban đầu năng suất người đó là 20 (sản phẩm/giờ)
Bài 22:
Gọi x (sản phẩm/giờ) là năng suất dự kiến của người đó \(\left(x\inℕ^∗;x< 20\right)\)
=> x + 1 (sản phẩm/giờ) là năng suất lúc sau của người đó
Theo bài ra ta có phương trình:
\(\frac{80}{x+1}-\frac{1}{5}=\frac{72}{x}\)
\(\Leftrightarrow400x-x\left(x+1\right)=360\left(x+1\right)\)
\(\Leftrightarrow400x-x^2-x=360x+360\)
\(\Leftrightarrow x^2-39x+360=0\)
\(\Leftrightarrow\left(x-15\right)\left(x-24\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-15=0\\x-24=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=15\left(tm\right)\\x=24\left(ktm\right)\end{cases}}\)
Vậy năng suất ban đầu là 15 sp/giờ
Gọi năng suất dự định là x
Năng suất thực tế là x+20
Thời gian thực tế là 120/x+20
Thời gian dự kiến là 120/x
Theo đề, ta có: \(\dfrac{120}{x}-\dfrac{125}{x+20}=1.5\)
=>120x+2400-125x=1,5x(x+20)
=>1,5x^2+35x=2400
=>x=30