Cho tam giác ABC, đường trung tuyến AM, tia phân giác của góc AMB cắt AB ở D, tia phân giác của góc AMC cắt AC ở E.
tam giác ABC cần thêm điều kiện gì để ta có DE=AM
mình cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xet ΔMAB co MD là phân giác
nen AD/DB=AM/MB=AM/MC
Xét ΔMCA có ME là phân giác
nên AE/EC=AM/MC=AD/DB
=>DE//BC
2: Xét ΔABM có DG//BM
nên DG/BM=AG/AM
Xét ΔACM có EG//MC
nên EG/MC=AG/AM
=>DG/BM=EG/MC
mà BM=MC
nên DG=EG
=>G là trung điểm của DE
Để G là trung điểm của AM thì ADME là hình bình hành
=>DM//AC
=>D là trung điểm của AB
=>E là trung điểm của BC
=>AM/MB=AD/DB=1
=>AM=1/2BC
=>góc BAC=90 độ

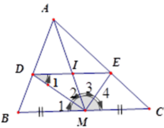
Vì MD và ME lần lượt là phân giác của A M B ^ , A M C ^ nên D A D B = M A M B , E A E C = M A M C
Mà MB = MC nên D A D B = E A E C => DE // BC (định lí Talet đảo)
Vì DE // BC nên D I B M = A I A M = I E M C (hệ quả định lí Talet) mà BM = MC nên DI = IE.
Nên cả A, B đều đúng.
Đáp án: D

1: Xét ΔAMB có MD là phân giác
nên AM/MB=AD/DB=AM/MC(1)
Xét ΔAMC có ME là phân giác
nên AM/MC=AE/EC(2)
Từ (1) và (2) suy ra AD/DB=AE/EC
hay DE//BC

1: Xét ΔAMB có MD là phân giác
nên AD/DB=AM/MB=AM/MC(1)
Xét ΔAMC cso ME là phân giác
nên AE/EC=AM/MC(2)
Từ (1)và (2) suy ra AD/DB=AE/EC
hay DE//BC

Áp dụng định lý phân giác cho tam giác ABM:
\(\dfrac{AM}{BM}=\dfrac{AD}{BD}\) (1)
Áp dụng định lý phân giác cho tam giác ACM:
\(\dfrac{AM}{CM}=\dfrac{AE}{CE}\) (2)
Mà AM là trung tuyến \(\Rightarrow BM=CM\) (3)
(1);(2);(3) \(\Rightarrow\dfrac{AD}{BD}=\dfrac{AE}{CE}\Rightarrow\dfrac{AD}{AD+BD}=\dfrac{AE}{AE+CE}\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
\(\Rightarrow DE||BC\) (định lý talet đảo)

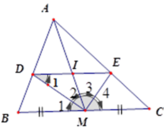
Vì DI = IE (cmt) nên MI là đường trung tuyến của tam giác MDE.
ΔMDE vuông (vì MD, ME là tia phân giác của góc kề bù) nên MI = DI = IE
Đặt DI = MI = x, ta có D I B M = A I A M (cmt) nên x 15 = 10 − x 10
Từ đó x = 6 suy ra DE = 12cm
Đáp án: D