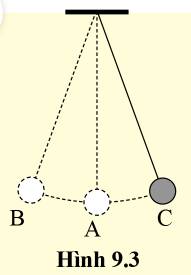
Một viên bi được treo ở đầu sợi dây nhẹ, dao động như hình 9.3. Vị trí cân bằng của viên bi là vị trí nào?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Chọn mốc thế năng tại vị trí cân bằng của con lắc.
Bỏ qua sức cản môi trường, cơ năng của con lắc được bảo toàn: W1 = W2
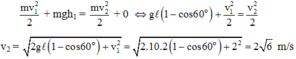

Chọn C.
Chọn mốc thế năng tại vị trí cân bằng của con lắc.
Bỏ qua sức cản môi trường, cơ năng của con lắc được bảo toàn: W 1 = W 2
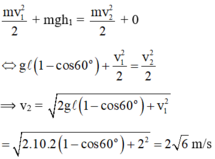

Biên độ: \(A=10cm\)
Tần số góc: \(\omega=10(rad/s)\)
Tại vị trí lò xo bị giãn \(5cm\) thì li độ của vật là: \(x=-10+5=-5cm\)
Vật đang đi lên là chuyển động theo chiều âm.
\(\Rightarrow \cos\varphi=-\dfrac{5}{10}=-0,5\)
\(\Rightarrow \varphi = \dfrac{2\pi}{3}\) (rad) (vì vật chuyển động theo chiều âm nên \(\varphi < 0\) )
PT dao động: \(x=10\cos(10t+\dfrac{2\pi}{3}) (cm)\)
Ở VTCB lò xo giãn 10 cm, như vậy để nó giãn 5cm thì từ VTCB phải đi lên 5cm.
Chiều dương hướng xuống, nên li độ lúc đó phải bằng -5cm.

Chọn A.
Chọn mốc thế năng tại vị trí cân bằng của con lắc.
Bỏ qua mọi ma sát, cơ năng của con lắc được bảo toàn: W1 = W2 = Wđmax
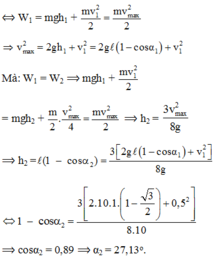

Chọn A.
Chọn mốc thế năng tại vị trí cân bằng của con lắc.
Bỏ qua mọi ma sát, cơ năng của con lắc được bảo toàn: W 1 = W 2 = W đ m a x
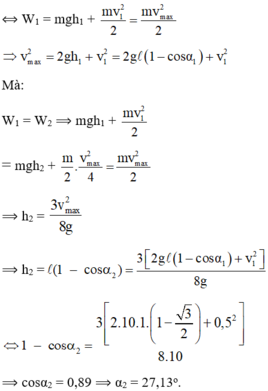

Đáp án A
Phương pháp: Đồng nhất với phương trình sóng dừng và áp dụng công thức tốc độ truyền sóng v = λ T
Cách giải:
Ta có: 2 π x λ = π x 4 ω = 20 π ⇒ v = λ T = 80 c m / s

Đáp án A
Phương pháp: Đồng nhất với phương trình sóng dừng và áp dụng công thức tốc độ truyền sóng v = λT
Cách giải:
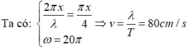
Vị trí cân bằng của viên bi là vị trí A