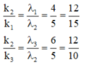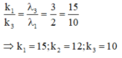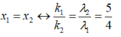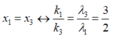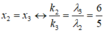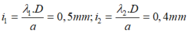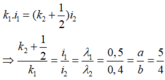Trong thí nghiệm Y-âng, nguồn phát đồng thời hai bức xạ λ1 = 0,4 µm và λ2 = 0,5 µm . M là điểm nằm trên màn có màu giống vân trung tâm O và gần O nhất. Xét OM c:
a) bao nhiêu vân sáng tạo ra
b) bao nhiêu vân tối tạo ra
c) bao nhiêu vân sáng quan sát được
d) bao nhiêu vân tối quan sát được
e)bao nhiêu vâm sáng có màu đơn sắc