Question

[Đoàn Đức Hà]

(2,5 điểm) Giải bài toán bằng cách lập hệ phương trình:

Trong tháng đầu, hai tổ sản xuất được $860$ chi tiết máy. Đến tháng thứ hai, tổ I vượt mức $15\%$, tổ II vượt mức $10\%$ do đó tháng hai cả hai tổ sản xuất được $964$ chi tiết máy. Tính số chi tiết máy mỗi tổ đã sản xuất được trong tháng đầu. 

Answer 1

[Nguyễn Đăng Nhân]

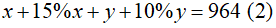
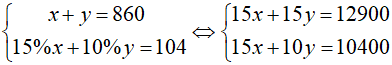
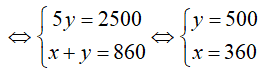
Gọi số máy tổ I và tổ II sản xuất được lần lượt là \(a,b\left(a,b\inℕ^∗;a,b< 860\right)\)ta có:

\(\left\{{}\begin{matrix}a+b=860\\\left(a+15\%a\right)+\left(b+10\%b\right)=964\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a+b=860\\\left(a+b\right)+\left(15\%a+10\%b\right)=964\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a+b=860\\860+\left(15\%a+10\%b\right)=964\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a+b=860\\15\%a+10\%b=104\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a+b=860\\10\%a+5\%a+10\%b=104\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a+b=860\\10\%\left(a+b\right)+5\%a=104\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a+b=860\\10\%\cdot860+10\%b=104\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a+b=860\\86+10\%b=104\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a+b=860\\10\%b=18\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a+b=860\\b=180\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}b=180\\a=a+b-b=860-180\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}b=180\\a=680\end{matrix}\right.\)

Vậy tổ 1 sản xuất được 680 máy trong tháng đầu, tổ 2 sản xuất được 180 máy trong tháng đầu.

Answer 2

[BAO UYEN8KT]