 Giúp mình câu 15
Giúp mình câu 15
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1 environmental
2 Polluting
3 conservation
4 consumption
5 appliances
6 innovation
7 Ultimately
8 suggestion
9 heated
10 environmentalists
11 worried
12protection
13 seriously
14 dripping
15 reducing


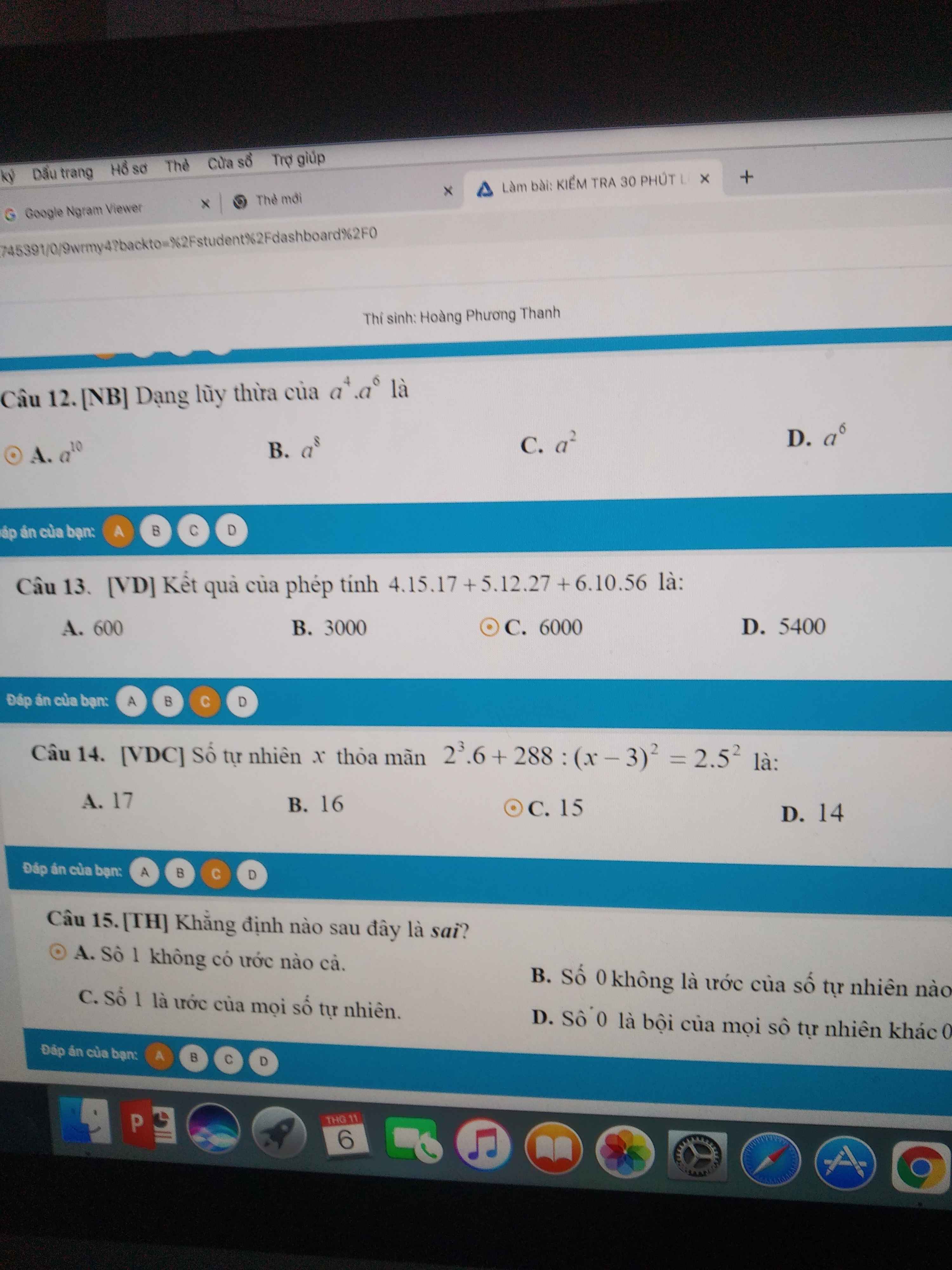
15.
\(V_{H_2O}=2V_{CO_2}\Rightarrow n_{H_2O}=2n_{CO_2}\Rightarrow\dfrac{n_{CO_2}}{n_{H_2O}}=\dfrac{1}{2}\)
Bảo toàn C: \(n_C=n_{CO_2}=1\left(mol\right)\)
Bảo toàn H: \(n_H=2n_{H_2O}=2.2=4\left(mol\right)\)
CT có dạng: \(\left(CH_4\right)n\)
\(\Leftrightarrow C_nH_{4n}\)
Ta có: \(4n\le2n+2\)
\(\Leftrightarrow n\le1\)
`->n=1` `->` CTPT Z: CH4
`->` Chọn D

1D 2B 3C 4A 5A 6C 7A 8A 9B 10A 11C 12D 13D 14D 15A 16D 17A 18C 19C 20D 21D 22C 23C 24A 25B 26C 27D 28B 29C






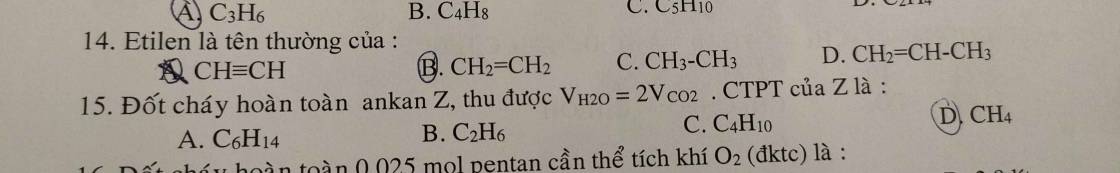


Câu 15:
Gọi CT chung là \(C_nH_{2n+2}\left(n>0\right)\)
\(M_{C_nH_{2n+2}}=18,5.2=37\left(g/mol\right)\)
\(\Rightarrow14n+2=37\Leftrightarrow n=2,5\)
`=>` 2 ankan là \(C_2H_6;C_3H_8\)
Áp dụng sơ đồ đường chéo:
\(\dfrac{n_{C_2H_6}}{n_{C_3H_8}}=\dfrac{44-37}{37-30}=\dfrac{1}{1}\Rightarrow\%V_{C_2H_6}=\%V_{C_3H_8}=\dfrac{1}{2}.100\%=50\%\)
Chọn C
Câu 16:
\(n_{CO_2}=\dfrac{0,44}{44}=0,01\left(mol\right);n_{H_2O}=\dfrac{0,21}{18}=\dfrac{7}{600}\left(mol\right)\)
Vì \(n_{H_2O}>n_{CO_2}\left(\dfrac{7}{600}>0,01\right)\Rightarrow\) A là ankan có CTPT là \(C_nH_{2n+2}\left(n\in N;n\ge1\right)\)
\(n_A=n_{H_2O}-n_{CO_2}=\dfrac{1}{600}\left(mol\right)\)
\(\left\{{}\begin{matrix}n_C=n_{CO_2}=0,01\left(mol\right)\\n_H=2n_{H_2O}=\dfrac{7}{300}\left(mol\right)\end{matrix}\right.\Rightarrow m_A=0,01.12+\dfrac{7}{300}=\dfrac{43}{300}\left(g\right)\)
`=>` \(M_{C_nH_{2n+2}}=\dfrac{\dfrac{43}{300}}{\dfrac{1}{600}}=86\left(g/mol\right)\)
`=>` \(14n+2=86\Leftrightarrow n=6\)
Vậy A là \(C_6H_{14}\)
Mà A tạo được 2 dẫn xuất monoclo
`=>` CTCT của A là \(CH_3-CH\left(CH_3\right)-CH\left(CH_3\right)-CH_3\) (2,3 - đimetylbutan0
Chọn C
Câu 17:
\(n_{C_4H_{10}}=\dfrac{5,8}{58}=0,1\left(mol\right)\\ \xrightarrow[]{BTNT:H}n_{H_2O}=5n_{C_4H_{10}}=0,5\left(mol\right)\\ \Rightarrow m_{H_2O}=0,5.18=9\left(g\right)\)