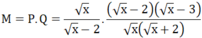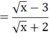Q(x) = 2x^2 +5x^4 +3/16. Tìm x để Q(x) = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có :
\(5x^4\ge0\forall x\)
\(2x^2\ge0\forall x\)
\(\Rightarrow5x^4+2x^2+\frac{3}{16}\ge\frac{3}{16}\forall x\)
\(\Rightarrow M\ge\frac{3}{16}\)
Nên : \(M\ne0\)
\(\Rightarrow\)Không có giá trị nào của \(x\)để \(M\left(x\right)=0\)
~ Ủng hộ nhé
Ta có: \(M\left(x\right)=5x^4+2x^2+\frac{3}{16}\)
\(M\left(x\right)\ge\frac{3}{16}\forall x.\)
Vậy không có giá trị nào của x để \(M\left(x\right)=0\) \(\Rightarrow\)M(x) vô nghiệm.
Kb vs cho tớ nhé mn! ^.^

b: =>(x+5)(x-3)=0
=>x=3 hoặc x=-5
c: \(\Leftrightarrow x\left(x^2-4x+5\right)=0\)
=>x=0
d: \(\Leftrightarrow2\cdot2^x-10\cdot2^x=-16\)
\(\Leftrightarrow-8\cdot2^x=-16\)
\(\Leftrightarrow2^x=2\)
hay x=1

a: \(P\left(x\right)=5x^5-4x^4-2x^3+4x^2+3x+6\)
Bậc là 5
\(Q\left(x\right)=-5x^5+4x^4+2x^3-4x^2+7x+\dfrac{1}{4}\)
Bậc là 5
b: H(x)=P(x)+Q(x)
\(=5x^5-4x^4-2x^3+4x^2+3x+6-5x^5+4x^4+2x^3-4x^2+7x+\dfrac{1}{4}\)
=10x+6,25
c: Để H(x)=0 thì 10x+6,25=0
hay x=-0,625


2: \(3x\left(x-4\right)+2x-8=0\)
=>\(3x\left(x-4\right)+2\left(x-4\right)=0\)
=>\(\left(x-4\right)\left(3x+2\right)=0\)
=>\(\left[{}\begin{matrix}x-4=0\\3x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-\dfrac{2}{3}\end{matrix}\right.\)
3: 4x(x-3)+x2-9=0
=>\(4x\left(x-3\right)+\left(x+3\right)\left(x-3\right)=0\)
=>\(\left(x-3\right)\left(4x+x+3\right)=0\)
=>\(\left(x-3\right)\left(5x+3\right)=0\)
=>\(\left[{}\begin{matrix}x-3=0\\5x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{3}{5}\end{matrix}\right.\)
4: \(x\left(x-1\right)-x^2+3x=0\)
=>\(x^2-x-x^2+3x=0\)
=>2x=0
=>x=0
5: \(x\left(2x-1\right)-2x^2+5x=16\)
=>\(2x^2-x-2x^2+5x=16\)
=>4x=16
=>x=4