Cho số phức Z thoả mãn (1+2i)z-5= 3i tìm số phức liên hợp z 2/ cho số phức z=a+bi(a, b thuộc R) thoả mãn 3z-5z ngan -6+10i=0 .tính a-b
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

17 tháng 7 2018
ta có : \(\left|z+1+i\right|=\left|z+2i\right|\Leftrightarrow\left(a+1\right)^2+\left(b+1\right)^2+a^2+\left(b+2\right)^2\)
\(\Leftrightarrow b=a-1\)
khí đó : \(P=\left|z-2-3i\right|+\left|z+1\right|=\sqrt{\left(a-2\right)^2+\left(b-3\right)^2}+\sqrt{\left(a+1\right)^2+b^2}\)
\(\Leftrightarrow P=\sqrt{\left(a-2\right)^2+\left(a-4\right)^2}+\sqrt{\left(a+1\right)^2+\left(a-1\right)^2}\ge\sqrt{\left(2a-1\right)^2+\left(2a-5\right)^2}\)
dấu "=" xảy ra khi \(\dfrac{a-2}{a+1}=\dfrac{a-4}{a-1}=k>0\) \(\Leftrightarrow a\in\varnothing\) \(\Rightarrow\) không có giá trị của \(P=a+2b\)
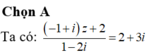
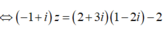
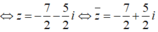
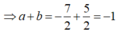
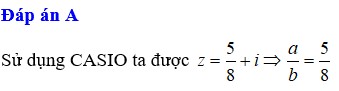



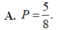
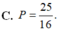
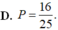
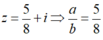
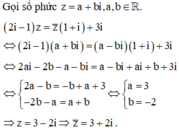

\(\left(1+2i\right)z-5=3i\Leftrightarrow\left(1+2i\right)z=5+3i\)
\(\Rightarrow z=\dfrac{5+3i}{1+2i}=\dfrac{11}{5}-\dfrac{7}{5}i\)
\(\Rightarrow\overline{z}=\dfrac{11}{5}+\dfrac{7}{5}i\)
2.
Đề câu này là: \(3z-5\overline{z}-6+10i=0\) đúng không nhỉ?