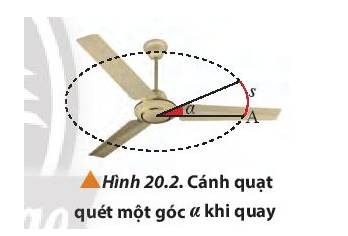
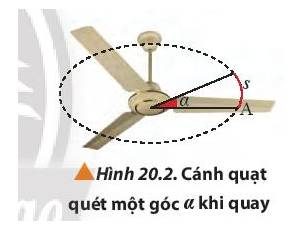
4. Ta cần lưu ý gì khi sử dụng công thức (20.2) để tính độ lớn của một góc chắn cung tròn có chiều dài s.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
KS
Kiều Sơn Tùng
7 tháng 9 2023
Đúng(0)
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
16 tháng 12 2023
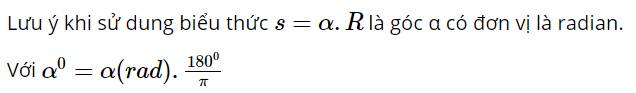
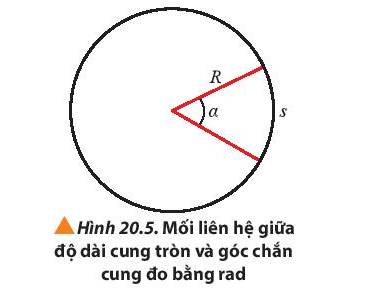
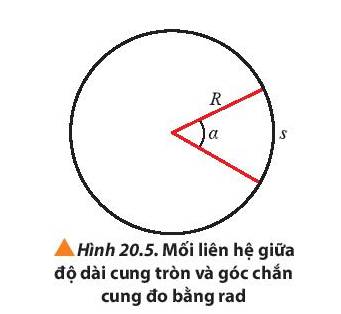
Lưu ý khi sử dung biểu thức \(s = \alpha .R\) là góc α có đơn vị là radian.
Với \({\alpha ^0} = \alpha (rad).\frac{{{{180}^0}}}{\pi }\)
QT
Quoc Tran Anh Le
Giáo viên
16 tháng 12 2023
Theo công thức tính chu vi đường tròn có bán kính R, ta có chiều dài của nửa đường tròn bằng πR.
Vì cung tròn của đường tròn có chiều dài là R tương ứng với góc 1 rad nên chiều dài tương ứng với góc π rad.
7 tháng 9 2023
Theo công thức tính chu vi đường tròn có bán kính R, ta có chiều dài của nửa đường tròn bằng πR.
Vì cung tròn của đường tròn có chiều dài là R tương ứng với góc 1 rad nên chiều dài tương ứng với góc π rad.
QT
Quoc Tran Anh Le
Giáo viên
16 tháng 12 2023
- Công thức tính chiều dài cung tròn s đã được học là: \(s = \frac{{\pi .R.\alpha }}{{180}}\)
- Trong công thức trên, α được tính theo đơn vị là độ.
- Công thức tính chiều dài đơn giản hơn: \(s = \alpha .R\); trong đó α có đơn vị là rad.
Với \({\alpha ^0} = \alpha (rad).\frac{{{{180}^0}}}{\pi }\)
20 tháng 2 2022
Công thực hiện:
\(A=P\cdot h=10m\cdot h=10\cdot500\cdot2=10000J\)
Hiệu suất \(75\%\) thì công thắng ma sát là:
\(H=\dfrac{A_i}{A_{tp}}\Rightarrow A_{tp}=\dfrac{A_i}{H}\cdot100\%=\dfrac{10000}{75\%}\cdot100\%=\dfrac{40000}{3}J\)
Công ma sát:
\(A_{ms}=A_{tp}-A_i=\dfrac{40000}{3}-10000=\dfrac{10000}{3}J\)
Độ lớn lực ma sát:
\(F_{ms}=\dfrac{A_{ms}}{l}=\dfrac{\dfrac{10000}{3}}{6}=\dfrac{5000}{9}\approx555,55N\)
TH
0
ML
1
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
8 tháng 11 2023
Khi sử dụng thuốc kháng sinh để điều trị các bệnh ở người, chúng ta cần lưu ý:
- Chỉ sử dụng kháng sinh khi thật sự bị bệnh nhiễm khuẩn.
- Phải chọn đúng loại, đúng liều kháng sinh.
- Phải dùng kháng sinh đủ thời gian: Tùy theo loại bệnh và tình trạng bệnh thời gian dùng kháng sinh có khi dài khi ngắn nhưng thông thường là không dưới 5 ngày.
→ Vậy khi dùng kháng sinh cần tuân thủ theo hướng dẫn của bác sĩ, không tự ý dùng thuốc kháng sinh để tránh hiện tượng nhờn thuốc, khó điều trị hơn.