1. Hãy tính động lượng và động năng của hệ trước và sau va chạm đàn hồi (Hình 29.1).
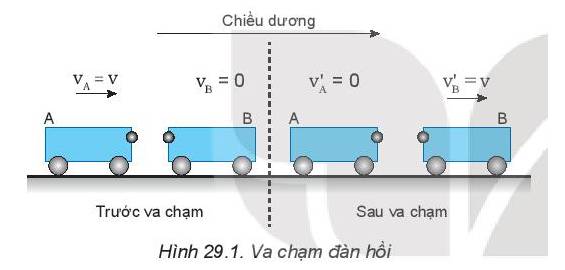
2. Từ kết quả tính được rút ra nhận xét gì?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
26 tháng 6 2017
Chọn chiều chuyển động ban đầu của quả cầu A là chiều dương. Hệ vật gồm hai quả cầu A và B. Gọi v 1 , v 2 và v ' 1 , v ' 2 là vận tốc của hai quả cầu trước và sau khi va chạm.
Vì hệ vật chuyển động không ma sát và ngoại lực tác dụng lên hệ vật (gồm trọng lực và phản lực của máng ngang) đều cân bằng nhau theo phương thẳng đứng, nên tổng động lượng của hệ vật theo phương ngang được bảo toàn (viết theo trị đại số):
m 1 v ' 1 + m 2 v ' 2 = m 1 v 1 + m 2 v 2
2. v ' 1 + 3. v ' 2 = 2.3 +3.1 = 9
Hay v ' 1 + 1,5. v ' 2 = 4,5 ⇒ v ' 2 = 3 - 2 v ' 1 /3 (1)
Đồng thời, tổng động năng của hệ vật cũng bảo toàn, nên ta có:
m1 v ' 1 2 /2 + m2 v ' 2 2 /2 = m1 v 1 2 /2 + m2 v 2 2 /2
2 v ' 1 2 /2 + 3 v ' 2 2 /2 = 2. 3 2 /2 + 3. 1 2 /2
Hay v ' 1 2 + 1,5 v ' 2 2 = 10,5 ⇒ v ' 2 2 = 7 - 2 v ' 1 2 /3 (2)
Giải hệ phương trình (1), (2), ta tìm được: v ' 1 = 0,6 m/s; v ' 2 = 2,6 m/s
(Chú ý: Loại bỏ cặp nghiệm v ' 1 = 3 m/s, v ' 2 = 1 m/s, vì không thỏa mãn điều kiện v ' 2 > v 2 = 1 m/s)
HQ
Hà Quang Minh
Giáo viên
3 tháng 11 2023
Khối lượng của hai xe là như nhau và đều có độ lớn là m = 0,245 (kg)
Động lượng của xe 1 trước va chạm: p1 = 0,444.m
Động lượng của xe 1 sau va chạm: p’1 = 0,316.m
=> Độ thay đổi động lượng của xe 1 là: \(\Delta {p_1} = \left| {p_1' - {p_1}} \right| = 0,444m - 0,316m \approx 0,03(kg.m/s)\)
Động lượng của xe 2 trước va chạm: p2 = 0,316.m
Động lượng của xe 2 sau va chạm: p’2 = 0,438.m
=> Độ thay đổi động lượng của xe 2 là: \(\Delta {p_2} = \left| {p_2' - {p_2}} \right| = 0,438m - 0,316m \approx 0,03(kg.m/s)\)
=> Độ thay đổi động lượng của xe 1 và xe 2 bằng nhau.
QT
Quoc Tran Anh Le
Giáo viên
14 tháng 12 2023
- Trong quá trình va chạm động lượng và động năng của hệ có được bảo toàn.
- Ngoài ra, những kiến thức về động lượng có thể được vận dụng trong thực tiễn như:
+ Hệ thống túi khí và đai an toàn trong ô tô giúp người ngồi trong xe hạn chế tối đa chấn thương khi xảy ra va chạm giao thông.
+ Vận động viên nhảy xa nhún chân, chùng đầu gối khi tiếp đất mục đích để tăng thời gian va chạm, giảm lực tác dụng.
+ Chế tạo hệ thống động cơ chuyển động bằng phản lực.
…
H9
HT.Phong (9A5)
CTVHS
5 tháng 5 2023
Bảo toàn động lượng ta có:
\(m_1v_1+m_2v_2=5m_1\)
\(\Leftrightarrow0,3v_1+0,1v_2=1,5\)
\(\Leftrightarrow3v_1+v_2=15\left(1\right)\)
Bảo toàn động năng lượng ta có:
\(\dfrac{1}{2}m_1v^2_1+\dfrac{1}{2}m_2v^2_2=\dfrac{25}{2}m_1\)
\(\Leftrightarrow3v^2_1+v_2^2=75\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}3v_1+v_2=15\\3v_1^2+v^2_2=75\end{matrix}\right.\)
Giải hệ phương trình ta được:
\(\left\{{}\begin{matrix}v_1=2,5m/s\\v_2=7,5m/s\end{matrix}\right.\)
QT
Quoc Tran Anh Le
Giáo viên
14 tháng 12 2023
Bảng số liệu: m1 = 0, 46 kg; m2 = 0,776 kg
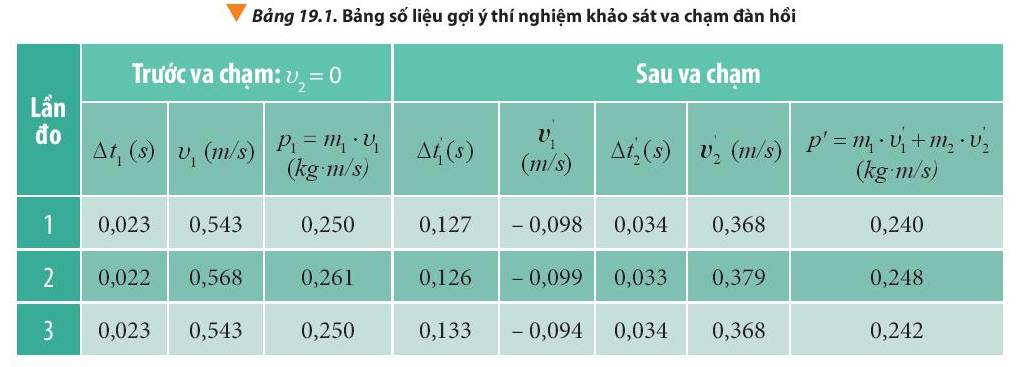
Bảng này, học sinh tự tính toán và thế vào bảng chính.
VT
6 tháng 10 2017
Đáp án: D
Gọi khối lượng, vận tốc của hạt nhân và của nơtron sau va chạm là M, V, m, v.
Vì va chạm là đàn hồi nên động năng của hệ trường hợp này được bảo toàn.
Ta có: MV + mv = mv0 (1); 
(2)
Giải hệ (1) và (2) ta tìm được: 
6 tháng 9 2023
Độ lớn động lượng trước và sau va chạm là: p = m.v = 0,06.28 = 1,68 (kg.m/s)
- Tính chất của vecto động lượng trước va chạm:
+ Hướng từ trái sang phải, hợp với phương ngang 1 góc 450
+ Độ lớn: p = 1,68 kg.m/s
- Tính chất của vecto động lượng sau va chạm:
+ Hướng từ phải sang trái, hợp với phương ngang 1 góc 450
+ Độ lớn: p = 1,68 kg.m/s
1.
- Động lượng của hệ trước va chạm: \({p_{tr}} = m.{v_A} = m.v\)
- Động lượng của hệ sau va chạm: \({p_s} = m.v_B' = m.v\)
- Động năng của hệ trước va chạm: \({W_{tr}} = \frac{1}{2}.m.v_A^2 = \frac{1}{2}.m.{v^2}\)
- Động năng của hệ sau va chạm: \({W_s} = \frac{1}{2}.m.v_B^{'2} = \frac{1}{2}.m.{v^2}\)
2.
Từ kết quả tính được, ta thấy trong va chạm đàn hồi, động lượng được bảo toàn, năng lượng được bảo toàn.