Bạn hãy phân tích lực tác dụng thành hai thành phần: thành phần vuông góc với phương dịch chuyển và thành phần trùng với phương dịch chuyển để lập luận rút ra biểu thức tính công.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
12 tháng 12 2023
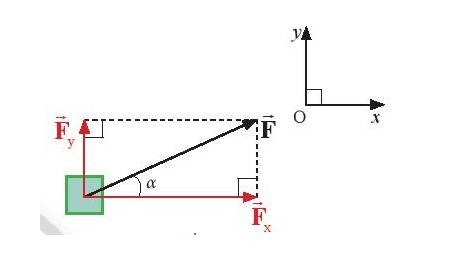
Ta có F = 12 N, α = 300
Độ lớn lực thành phần:
+ Fx = F.cosα = 12.cos300 = \(6\sqrt 3 \)(N).
+ Fy = F.sinα = 12.sin300 = 6 (N).
VT
6 tháng 9 2017
Chọn đáp án B
F1 và F2 là hai lực vuông góc với nhau nên ta có:
HQ
Hà Quang Minh
Giáo viên
3 tháng 11 2023
a)
Giản đồ vectơ các lực tác dụng lên thùng hàng:
b)
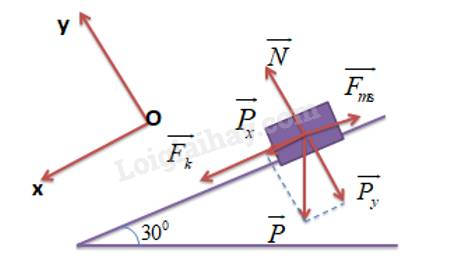
Ta có:
\({P_x} = P.\sin \alpha = 500.\sin {30^0} = 250N\)
\({P_y} = P.\cos \alpha = 500.\cos {30^0} = 500.\frac{{\sqrt 3 }}{2} = 250\sqrt 3 N\)
c)
Lực pháp tuyến của dốc lên thùng hàng không có tác dụng kéo thùng hàng xuống dốc vì nó cân bằng với thành phần \(\overrightarrow {{P_y}} \) của trọng lực.
d)
Chiếu các lực tác dụng lên trục Ox ta được:
\({F_k} - {F_{ms}} = ma \Leftrightarrow {F_k} - \mu N = ma\) (1)
Chiếu các lực tác dụng lên trục Oy ta được:
\(N - P.\cos \alpha = 0 \Leftrightarrow N = P.\cos \alpha = 250\sqrt 3 N\) (2)
Thay vào (1) ta được:
\(250 - \mu .250\sqrt 3 = \frac{{500}}{{10}}.2,00\)
\( \Leftrightarrow \mu = \frac{{150}}{{250\sqrt 3 }} = \frac{{\sqrt 3 }}{5} \approx 0,346\)
Vậy hệ số ma sát trượt giữa mặt dốc và thùng hàng là 0,346.
HB
16 tháng 4 2017
Khi vật M chuyển động thì các hình chiếu Mx và My của nó trên hai trục toạ độ cũng chuyển động theo
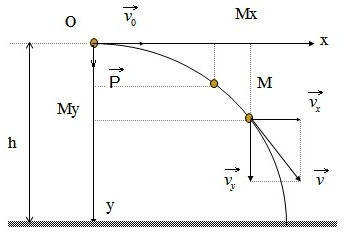
Thời gian chuyển động tổng hợp bằng thời gian chuyển động thành phần theo trục Oy. Suy ra thời gian chuyển động ném ngang của vật bằng thời gian rơi rự do từ cùng một độ cao.
\(t=\sqrt{\dfrac{2h}{y}}\)
HV
16 tháng 4 2017
Khi vật M chuyển động thì các hình chiếu Mx và My của nó trên hai trục toạ độ cũng chuyển động theo
Thời gian chuyển động tổng hợp bằng thời gian chuyển động thành phần theo trục Oy. Suy ra thời gian chuyển động ném ngang của vật bằng thời gian rơi rự do từ cùng một độ cao.
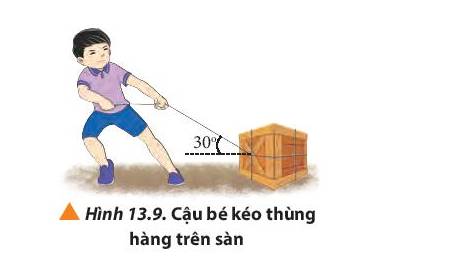
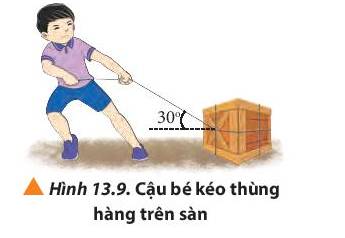
Khi người đẩy xe hàng để nó chuyển động theo chiều dương của trục Ox, lực đẩy \(\overrightarrow F \)làm hướng chuyển động một góc α bất kì. Ta phân tích lực \(\overrightarrow F \)ra hai lực thành phần vuông góc với nhau; \(\overrightarrow {{F_s}} \)cùng hướng chuyển động với vật và \(\overrightarrow {{F_n}} \)và \(\overrightarrow {{F_n}} \) vuông góc với \(\overrightarrow {{F_s}} \)
Trong trường hợp này chỉ có thành phần \(\overrightarrow {{F_s}} \)làm vật chuyển động nên công thức tính công là:
A = Fs .s = F.cosα.s = F.s.cosα