Biểu diễn quy tắc cộng vectơ cho trường hợp lực F2 ngược chiều với lực F1 khi F1 > F2 và khi F1 < F2.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng công thức: \(F^2=F_1^2+F_2^2+2.F_1.F_2.\cos\left(\widehat{F_1;F_2}\right)\)
a/ \(\overrightarrow{F_1}\uparrow\uparrow\overrightarrow{F_2}\Rightarrow\left(\widehat{F_1;F_2}\right)=0\Rightarrow\cos0=0\)
Thay số vào tìm đc F
b/ \(\overrightarrow{F_1}\uparrow\downarrow\overrightarrow{F_2}\Rightarrow\left(\widehat{F_1;F_2}\right)=180^0\Rightarrow\cos\left(\widehat{F_1;F_2}\right)=-1\)
Thay vào
c/ \(\left(\widehat{F_1;F_2}\right)=90^0\Rightarrow\cos90^0=0\)
d/ làm tương tự

Ta có F → = F → 1 + F → 2
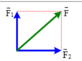
Trường hợp 1: ( F 1 → ; F → 2 ) = 0 0
⇒ F = F 1 + F 2 ⇒ F = 100 + 100 = 200 N
![]()
Trường hợp 2: ( F 1 → ; F → 2 ) = 60 0
⇒ F = 2. F 1 cos α 2 = 2.100. cos 60 0 2
⇒ F = 2.100. 3 2 = 100 3 ( N )
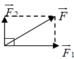
Trường hợp 3: ( F 1 → ; F → 2 ) = 90 0
⇒ F 2 = F 1 2 + F 2 2
⇒ F 2 = 100 2 + 100 2
⇒ F = 100 2 ( N )
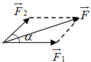
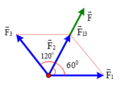
Trường hợp 4: ( F 1 → ; F → 2 ) = 120 0
⇒ F 2 = F 1 2 + F 2 2 + 2 F 1 F 2 cos α
⇒ F 2 = 100 2 + 100 2 + 2.100.100 cos 120 0
⇒ F = 100 ( N )
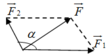
Trường hợp 5: ( F 1 → ; F → 2 ) = 180 0
⇒ F = F 1 − F 2 ⇒ F = 100 − 100 = 0 ( N )
![]()

1/ Khi \(\overrightarrow{F_1}\uparrow\uparrow\overrightarrow{F_2}\Rightarrow\cos\left(\widehat{F_1;F_2}\right)=\cos0=0\)
\(\Rightarrow F^2=F_1^2+F_2^2\Leftrightarrow F=\sqrt{6^2+6^2}=6\sqrt{2}\left(N\right)\)
2/ \(F^2=F_1^2+F_2^2+2.F_1.F_2.\cos\left(\widehat{F_1;F_2}\right)\)
\(F=\sqrt{6^2+6^2+2.6.6.\cos120}=6\left(N\right)\)

Ta có F → = F → 1 + F → 2
Trường hợp 1: ( F 1 → ; F → 2 ) = 0 0
⇒ F = F 1 + F 2 ⇒ F = 40 + 30 = 70 N
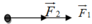
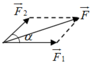
Trường hợp 2: ( F 1 → ; F → 2 ) = 60 0
⇒ F 2 = F 1 2 + F 2 2 + 2 F 1 F 2 cos α
⇒ F 2 = 40 2 + 30 2 + 2.40.30 cos 60 0
⇒ F = 10 37 N
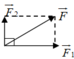
Trường hợp 3: ( F 1 → ; F → 2 ) = 90 0
⇒ F 2 = F 1 2 + F 2 2
⇒ F 2 = 40 2 + 30 2
⇒ F = 50 N
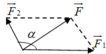
Trường hợp 4: ( F 1 → ; F → 2 ) = 120 0
⇒ F 2 = F 1 2 + F 2 2 + 2 F 1 F 2 cos α
⇒ F 2 = 40 2 + 30 2 + 2.40.30 cos 120 0
⇒ F = 10 13 N
Trường hợp 5: ( F 1 → ; F → 2 ) = 180 0
⇒ F = F 1 − F 2 ⇒ F = 40 − 30 = 10 N
Ta nhận thấy α càng lớn thì F càng nhỏ đi


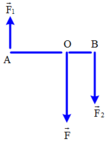
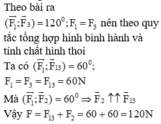
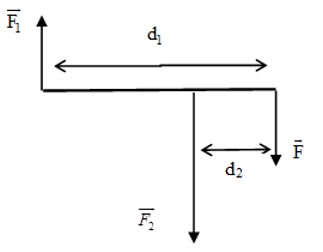

- TH1: \({F_1} > {F_2}\)
- TH2: \({F_1} < {F_2}\)