1 nhóm học sinh có 10 bạn, trong đó có 7 nữ 3 nam xếp hàng ngang. biết 2 bạn nam bất kỳ không được ở cạnh nhau. hỏi có bao nhiêu cách xếp hàng?
làm ơn giải giúp mình, mình tick cho =((((((((((((9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Coi 3 bạn nữ như 1 người
Số cách xếp là:
\(8!\cdot3!\)(cách)
b: Số cách xếp là:
\(10!-8!\cdot3!\left(cách\right)\)

Đáp án B

Số cách xếp 10 học sinh vào 10 ghế là: 10!
4 bạn nữ chỉ có thể xếp vào các vị trí N1,N2,N3,N4
Nếu Huyền ở vị trí N1 thì có 3! cách xếp 3 bạn nữ còn lại, Quang có 5 cách chọn chỗ ngồi và có 5! cách xếp 5 bạn nam còn lại. Vậy có 3!.5.5! = 3600 cách xếp
Tương tự nếu Huyền ở vị trí N4 cũng có 3600 cách xếp
Nếu Huyền ở vị trí N2 thì có 3! cách xếp 3 bạn nữ còn lại, Quang có 4 cách chọn chỗ ngồi và có 5! cách xếp 5 bạn nam còn lại. Vậy có 3!.4.5! = 2880 cách xếp
Tương tự nếu Huyền ở vị trí N3 cũng có 2880 cách xếp
Vậy có 2(3600 + 2880) = 12960 cách xếp thỏa mãn đề bài
⇒ p = 12960 10 ! = 1 280

Đáp án B
Số cách xếp 10 học sinh vào 10 ghế là: 10!
4 bạn nữ chỉ có thể xếp vào các vị trí N1,N2,N3,N4
Nếu Huyền ở vị trí N1 thì có 3! cách xếp 3 bạn nữ còn lại
Quang có 5 cách chọn chỗ ngồi và có 5! cách xếp 5 bạn nam còn lại
Vậy có 3!.5.5! = 3600 cách xếp
Tương tự nếu Huyền ở vị trí N4 cũng có 3600 cách xếp
Nếu Huyền ở vị trí N2 thì có 3! cách xếp 3 bạn nữ còn lại
Quang có 4 cách chọn chỗ ngồi và có 5! cách xếp 5 bạn nam còn lại
Vậy có 3!.4.5! = 2880 cách xếp
Tương tự nếu Huyền ở vị trí N3 cũng có 2880 cách xếp
Vậy có 2(3600+2880) = 12960 cách xếp thỏa mãn đề bài
⇒ p = 12960 10 ! = 1 280

Đáp án B
Kí hiệu 10 ghế như sau:
Trong đó: D là ghế đỏ (dành cho nữ) và X là ghế xanh (dành cho nam)
+ Số cách xếp nữ vào ghế đỏ, nam vào ghế xanh là M = 4!6!
+ Số cách xếp sao cho Quang được ngồi cạnh Huyền (kí hiệu là N)
- Chọn 2 ghế liên tiếp khác màu: C 6 1 cách
- Xếp Quang và Huyền vào 2 ghế đó (1 cách) và xếp các bạn kia vào các ghế còn lại (3!5! cách)
=> N = 3!5!.6 => N = 3!.6!
+ Số cách xếp thỏa mãn điều kiện đề bài là M – N = 12960 cách
Xác suất cần tìm là 12960 10 ! = 1 280 .

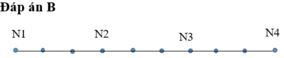
Số cách xếp 10 học sinh vào 10 ghế là: 10!
4 bạn nữ chỉ có thể xếp vào các vị trí N1,N2,N3,N4
Nếu Huyền ở vị trí N1 thì có 3! cách xếp 3 bạn nữ còn lại, Quang có 5 cách chọn chỗ ngồi và có 5! cách xếp 5 bạn nam còn lại. Vậy có 3!.4.5! = 2880 cách xếp
Tương tự nếu Huyền ở vị trí N4 cũng có 3600 cách xếp
Nếu Huyền ở vị trí N2 thì có cách xếp 3 bạn nữ còn lại, Quang có 4 cách chọn chỗ ngồi và có cách xếp 5 bạn nam còn lại. Vậy có 2(3600 + 2880)= 12960 cách xếp
Tương tự nếu Huyền ở vị trí N3 cũng có 2880 cách xếp
Vậy có cách xếp thỏa mãn đề bài
⇒ p = 12960 10 ! = 1 280
39 cách
Tìm GTNN của A=|x-1|+|x-10|+|x-20|