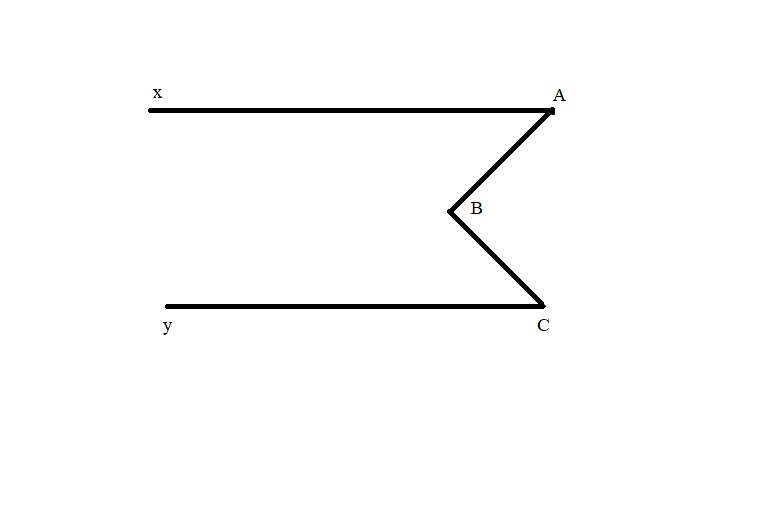
Cho hình vẽ, biết \hat{ABC}$ = \hat{A}$ + \hat{C}$. Chứng minh Ax//By
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Theo định lý sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} \to b = \frac{{a.\sin B}}{{\sin A}}\) thay vào \(S = \frac{1}{2}ab.\sin C\) ta có:
\(S = \frac{1}{2}ab.\sin C = \frac{1}{2}a.\frac{{a.\sin B}}{{\sin A}}.sin C = \frac{{{a^2}\sin B\sin C}}{{2\sin A}}\) (đpcm)
b) Ta có: \(\hat A + \hat B + \hat C = {180^0} \Rightarrow \hat A = {180^0} - {75^0} - {45^0} = {60^0}\)
\(S = \frac{{{a^2}\sin B\sin C}}{{2\sin A}} = \frac{{{{12}^2}.\sin {{75}^0}.\sin {{45}^0}}}{{2.\sin {{60}^0}}} = \frac{{144.\frac{1}{2}.\left( {\cos {{30}^0} - \cos {{120}^0}} \right)}}{{2.\frac{{\sqrt 3 }}{2}\;}} = \frac{{72.(\frac{{\sqrt 3 }}{2}-\frac{{-1 }}{2}})}{{\sqrt 3 }} = 36+12\sqrt 3 \)
30 tháng 11 2023
c: Gọi giao điểm của BC với Ax là K
BC\(\perp\)AC tại C
=>AC\(\perp\)BK tại K
=>ΔACK vuông tại C
\(\widehat{DKC}+\widehat{DAC}=90^0\)(ΔACK vuông tại C)
\(\widehat{DCK}+\widehat{DCA}=\widehat{KCA}=90^0\)
mà \(\widehat{DCA}=\widehat{DAC}\)(ΔDAC cân tại D)
nên \(\widehat{DKC}=\widehat{DCK}\)
=>DC=DK
mà DC=DA
nên DK=DA
=>D là trung điểm của AK
CH\(\perp\)AB
AK\(\perp\)AB
Do đó: CH//AK
Xét ΔOKD có CI//KD
nên \(\dfrac{CI}{KD}=\dfrac{OI}{OD}\left(1\right)\)
Xét ΔOAD có IH//AD
nên \(\dfrac{IH}{AD}=\dfrac{OI}{OD}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{CI}{KD}=\dfrac{IH}{AD}\)
mà KD=AD
nên CI=IH
=>I là trung điểm của CH
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
20 tháng 11 2023
A B E D C K
Ta có
\(AC=2AB\Rightarrow AB=\dfrac{AC}{2}\)
Gọi K là trung điểm AC
\(\Rightarrow AK=CK=\dfrac{AC}{2}\)
\(\Rightarrow AB=AK\) => tg ABK cân tại A
Ta có
\(\widehat{BAD}=\widehat{CAD}\) (gt)
\(\Rightarrow AD\perp BK\) (trong tg cân đường phân giác của góc ở đỉnh tg cân đồng thời là đường cao) (1)
Xét tg ACE có
AK=CK; BE=BC (gt) => BK là đường trung bình của tg ACE
=> BK//AE (2)
Từ (1) và (2) => \(AD\perp AE\Rightarrow\widehat{DAE}=90^o\) (Hai đường thẳng // nếu đường thẳng thứ 3 vuông góc với 1 trong 2 đường thẳng cho trước thì vuông góc với đường thẳng còn lại)
Cho hình vẽ, biết góc ABC = góc A + góc C. Chứng minh Ax//By
vt lại đề bài ik pro