help mình với ạaaaa
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1 :
a, Ta có : EF//BC
Theo định lý Ta-lét, ta có :
\(\Rightarrow\dfrac{AE}{EB}=\dfrac{AF}{FC}\)
hay \(\dfrac{4}{BE}=\dfrac{6}{3}\)
\(\Rightarrow BE=\dfrac{4.3}{6}=2\)
b, Ta có : DK là phân giác \(\widehat{EDF}\) ( hình hơi mờ và còn sai góc nữa bạn)
\(\Rightarrow\dfrac{EK}{KF}=\dfrac{ED}{DF}\)
hay \(\dfrac{EK}{KF}=\dfrac{12}{16}=\dfrac{3}{4}\)
\(\Rightarrow\dfrac{EK}{3}=\dfrac{KF}{4}=\dfrac{EK+KF}{3+4}=\dfrac{18}{7}\)
\(\Rightarrow EK=\dfrac{18}{7}.3=\dfrac{54}{7}\)
\(\Rightarrow KF=\dfrac{18}{7}.4=\dfrac{72}{7}\)

1)
a) \(2\sqrt{50}-3\sqrt{2}+\dfrac{1}{3}\sqrt{18}\)
\(=2\cdot5\sqrt{2}-3\sqrt{2}+\dfrac{1}{3}\cdot3\sqrt{2}\)
\(=10\sqrt{2}-3\sqrt{2}+\sqrt{2}\)
\(=8\sqrt{2}\)
b) \(\dfrac{11}{4-\sqrt{5}}-\dfrac{3}{\sqrt{5}+\sqrt{2}}\)
\(=\dfrac{11\left(4+\sqrt{5}\right)}{\left(4-\sqrt{5}\right)\left(4+\sqrt{5}\right)}-\dfrac{3\left(\sqrt{5}-\sqrt{2}\right)}{\left(\sqrt{5}+\sqrt{2}\right)\left(\sqrt{5}-\sqrt{2}\right)}\)
\(=\dfrac{11\left(4+\sqrt{5}\right)}{16-5}-\dfrac{3\left(\sqrt{5}-\sqrt{2}\right)}{5-2}\)
\(=\dfrac{11\left(4+\sqrt{5}\right)}{11}-\dfrac{3\left(\sqrt{5}-\sqrt{2}\right)}{3}\)
\(=4+\sqrt{5}-\sqrt{5}+\sqrt{2}\)
\(=4+\sqrt{2}\)
c) \(\sqrt{8-2\sqrt{15}}-\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}\)
\(=\sqrt{\left(\sqrt{5}\right)^2-2\cdot\sqrt{5}\cdot\sqrt{3}+\left(\sqrt{3}\right)^2}-\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}\)
\(=\sqrt{\left(\sqrt{5}-\sqrt{3}\right)^2}-\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}\)
\(=\left|\sqrt{5}-\sqrt{3}\right|-\left|\sqrt{5}+\sqrt{3}\right|\)
\(=\sqrt{5}-\sqrt{3}-\sqrt{5}-\sqrt{3}\)
\(=-2\sqrt{3}\)


Giá tiền mua 1 lít dầu hết số tiền là: \(50000\div2,5=20000\left(đ\right)\)
Đáp số: 20000 đồng
giá tiền 1\(l\) dầu là
50 000 \(\div\) 2,5 = 2000 ( \(^đ\) )
Đáp số : 2000\(^đ\)

Bài 1:
\(A=2\cos 60^0-2\sin 30^0+\cot 45^0=2\sin (90^0-60^0)-2\sin 30^0+\cot 45^0\)
\(=\cot 45^0=1\)
\(B=\tan 35^0.\cot 35^0=1\)
\(C=\sin ^235^0+\sin ^265^0=\sin ^235^0+[\cos (90^0-65^0)]^2=\sin ^235^0+\cos ^235^0=1\)
Bài 2:
a. Áp dụng công thức $\cos a=\sin (90^0-a)$ nên:
\(\sin 25^0, \cos 42^0, \sin 47^0, \cos 15^0,\sin 38^0\) viết lại thành:
\(\sin 25^0, \sin 48^0, \sin 47^0, \sin 75^0, \sin 38^0\)
Do đó thứ tự từ bé đến lớn là:
$\sin 25^0, \sin 38^0, \sin 47^0, \cos 42^0, \cos 15^0$
b. Sử dụng công thức: $\cot x=\tan (90^0-x)$ thì:
\(\tan 42^0, \cot 61^0, \tan 28^0, \cot 79^01', \tan 35^0\) viết thành:
$\tan 42^0, \tan 29^0, \tan 28^0, \tan 10^059', \tan 35^0$
Do đó thứ tự từ bé đến lớn là:
$\cot 79^01', \tan 28^0, \cot 61^0, \tan 35^0,\tan 42^0$
c.
\(\sin 15^0, \cot 20^0, \tan 60^0, \sin 50^0, \cos 30^0\) viết lại thành:
\(\sin 15^0, \tan 70^0, \tan 60^0, \sin 50^0,\sin 60^0\)
Mà:
\(\tan 60^0=\frac{\sin 60^0}{\cos 60^0}>\sin 60^0\)
\(\tan 70^0> \tan 60^0\). Do đó sắp xếp theo thứ tự từ bé đến lớn là:
$\sin 15^0, \sin 50^0, \cos 30^0, \tan 60^0, \cot 20^0$


Lời giải:
Gọi vận tốc ban đầu là $x$ km/h
Thời gian dự định: $\frac{AB}{x}$ (h)
Khi vận tốc tăng $a$ km/h thì thời gian đi là: $\frac{AB}{x+a}$ (h)
$\frac{AB}{x}-\frac{AB}{x+a}=0,5$
$\Leftrightarrow \frac{aAB}{x(x+a)}=0,5(*)$
Khi vận tốc giảm $b$ km/h thì thời gian đi là: $\frac{AB}{x-b}$ (h)
$\frac{AB}{x-b}-\frac{AB}{x}=1$
$\Leftrightarrow \frac{bAB}{x(x-b)}=1(**)$
Từ $(*); (**)\Rightarrow \frac{x-b}{x+a}.\frac{a}{b}=0,5$
$\Leftrightarrow 2a(x-b)=b(x+a)$
$\Leftrightarrow 2ax-2ab=bx+ab$
$\Leftrightarrow x(2a-b)=3ab$
$\Rightarrow x=\frac{3ab}{2a-b}$
Đến đây bạn thay $a,b$ vô để tính thôi.

uses crt;
var n,i,s:integer;
begin
clrscr;
n:=1;
s:=0;
repeat
s:=s+n;
n:=n+1;
until s>1000;
writeln(n);
readln;
end.


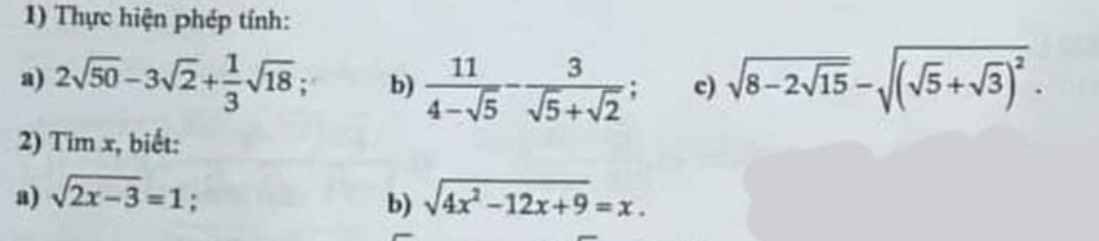



Gọi tọa độ của M là: \(M_{\left(x;y\right)}\)
Ta có: \(\left\{{}\begin{matrix}\overrightarrow{MA}_{\left(-2-x;4-y\right)}\\\overrightarrow{MB}_{\left(1-x;-y\right)}\\3\overrightarrow{MC}_{\left(9-3x;-6-3y\right)}\end{matrix}\right.\)
\(\overrightarrow{MA}+\overrightarrow{MB}=3\overrightarrow{MC}\)
Ta lại có: \(\left(\overrightarrow{MA}+\overrightarrow{MB}\right)_{\left(-1-2x;4-2y\right)}\)
Suy ra: \(\left\{{}\begin{matrix}-1-2x=9-3x\\4-2y=-6-3y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=10\\y=-10\end{matrix}\right.\)
Vậy tọa độ điểm M là: \(M_{\left(10;-10\right)}\)