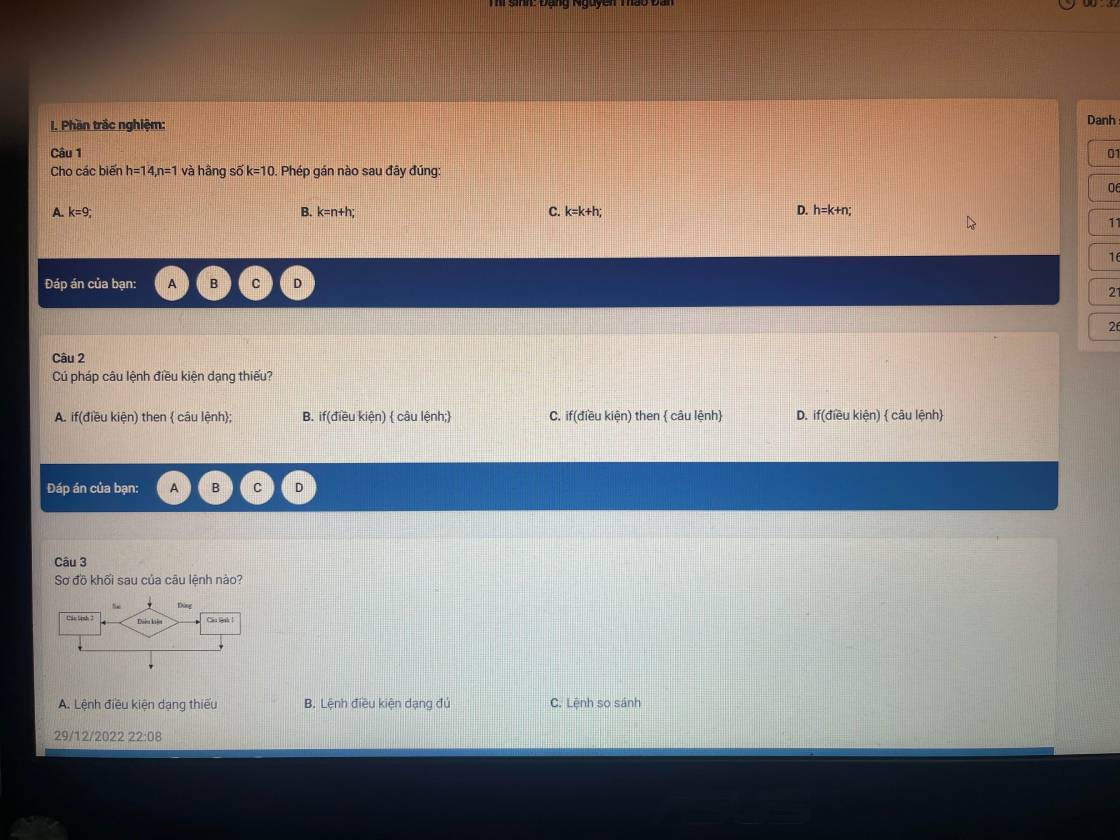
Giúp m và ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DH
21 tháng 2 2021
gọi đường thẳng qua M là Δ có vecto n là (a;b) đk a2+b2 ≠ 0
PTTQ của đg đi qua M là a(x-1)+b(y-2)=0 *
ta có CT tính góc giữa hai 2 đt
cos (Δ ;d ) = \(\dfrac{\left|3a-2b\right|}{\sqrt{a^2+b^2}.\sqrt{3^2+\left(-2\right)^2}}=\dfrac{\sqrt{2}}{2}\)
\(2\left|3a-2b\right|=\sqrt{26}\sqrt{a^2+b^2}\)
\(4\left(9a^{2^{ }}+4b-12ab\right)=26\sqrt{a^2+b^2}\)
\(10a^2-48ab-10b^2=0\)
(hd bấm máy tính bạn bấm pt bậc 2 các hệ số lần lượt là a = 10 ,b=-48,c=-10 ra kq là x= 5 và -1:5 ròi ghi a=5b và a=-1:5b nha )
\(\left[{}\begin{matrix}a=5b\\a=-\dfrac{1}{5}b\end{matrix}\right.\)
th1 vs a=5b
chọn b=1 =>a =5 thế vào * => pt đt qua M (ở đây bạn thích chọn b= số nào cx đc nha mình chọn 1 vì tốn giản thôi ở dưới cx tương tự )
th2 vs a=-\(\dfrac{1}{5}\)b
chọn b=-5 => a = 1 thế vào * => pt đt qua M
C
1
27 tháng 12 2021
bn vào olm.vn ik trong đấy có câu trả lời đấy!
gợi ý cho bn r đó nha !
nhớ like cho mik đấy!
27 tháng 12 2021
Ta có \(m=\dfrac{3^p-1}{2}\cdot\dfrac{3^p+1}{4}=ab\) với \(\left(a;b\right)=\left(\dfrac{3^p-1}{2};\dfrac{3^p+1}{4}\right)\)
Vì \(a,b\) là các số nguyên lớn hơn 1 nên m là hợp số
Mà \(m=9^{p-1}+9^{p-2}+...+9+1\) và p lẻ nên \(m\equiv1\left(mod3\right)\)
Theo định lí Fermat, ta có \(\left(9^p-9\right)⋮p\)
Mà \(\left(p,8\right)=1\Rightarrow\left(9^p-9\right)⋮8p\Rightarrow m-1⋮\dfrac{9^p-9}{8}⋮p\)
Vì \(\left(m-1\right)⋮2\Rightarrow\left(m-1\right)⋮2p\Rightarrow\left(3^{m-1}-1\right)⋮\left(3^{2p}-1\right)⋮\dfrac{9^p-1}{8}=m\left(đpcm\right)\)
AH
Akai Haruma
Giáo viên
16 tháng 7 2023
Lời giải:
Lần sau bạn nhớ ghi đầy đủ đề. $ABC$ là tam giác vuông tại $A$.
$\frac{AB}{AC}=\frac{3}{4}$
$\Rightarrow AC=\frac{4AB}{3}=\frac{4.15}{3}=20$ (cm)
Áp dụng định lý Pitago:
$y=BC=\sqrt{AB^2+AC^2}=\sqrt{15^2+20^2}=25$ (cm)
$S_{ABC}=AB.AC:2=AH.BC:2$
$\Rightarrow AB.AC=AH.BC$
$\Rightarrow x=AH=\frac{AB.AC}{BC}=\frac{15.20}{25}=12$ (cm)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
28 tháng 11 2023
n.m=36
=> n.(-m)= n.m.(-1)=36.(-1)= -36
(-n).(-m)= n.m. (-1). (-1)= n.m.1= 36.1=36
PT
2
26 tháng 7 2021
ta có: M=10^2020 +1 / 10^2019 +1
=> M/10= 10^2020 +1 / 10( 10^2019 +1 )
= 10^2020+1/ 10^2020 +10
=> 10/A= 10^2020 +10/10^2020 +1
=(10^2020 +1) +9/ 10^2020+1
=10^2020+1 /10^2020+1 + 9/10^2020+1
=1+ 9/10^2020+1
ta lại có: N=10^2021 +1/10^2020 +1
=> N/10= 10^2021+1/ 10(10^2020+1)
= 10^2021+1 / 10^2021+10
=> 10/N=10^2021+10 / 10^2021+1
=(10^2021+1) +9/10^2021+1
=10^2021+1/10^2021+1 +9/10^2021+1
=1+ 9/10^2021+1
ta thấy: 10/M>10N
=>M<N
26 tháng 7 2021
\(M=\dfrac{10^{2020}+1}{10^{2019}+1}=1-\dfrac{9}{10^{2019}+1}\)
\(N=\dfrac{10^{2021}+1}{10^{2020}+1}=1-\dfrac{9}{10^{2020}+1}\)
Ta có: \(10^{2019}+1< 10^{2020}+1\)
\(\Leftrightarrow\dfrac{9}{10^{2019}+1}>\dfrac{9}{10^{2020}+1}\)
\(\Leftrightarrow-\dfrac{9}{10^{2019}+1}< -\dfrac{9}{10^{2020}+1}\)
\(\Leftrightarrow M< N\)
B
6 tháng 3 2022
Fe+2HCl->Fecl2+H2
0,05---0,1--------------0,05
FeO+2HCl->Fecl2+H2
0,1------0,2
n H2=\(\dfrac{1,12}{22,4}\)=0,05 mol
n HCl=1.0,3=0,3 mol
=>m Fe=0,05.56=2,8g
=>n FeO=0,1.72=7,2g
=>m =2,8+7,2=10g
6 tháng 3 2022
nHCl = 0,3 . 1 = 0,3 (mol)
nH2 = 1,12/22,4 = 0,05 (mol)
PTHH: Fe + 2HCl -> FeCl2 + H2
Mol: 0,05 <--- 0,1 <--- 0,05 <--- 0,05
nHCl (FeO) = 0,3 - 0,1 = 0,2 (mol)
PTHH: FeO + 2HCl -> FeCl2 + H2
Mol: 0,1 <--- 0,2
m = 0,05 . 56 + 0,1 . 72 = 10 (g)
MA
các bạn giải giúp m với ạ! Mình đang cần gấp bài 2 và bài 3II
0
2A
3B