n2+2n
n4+3n2+1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 11 2019
Chia cả tử và mẫu của phân thức cho n 3 ( n 3 là lũy thừa bậc cao nhất của n trong phân thức), ta được:
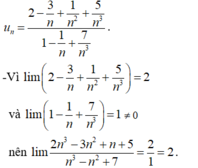
Chọn C.
CM
3 tháng 8 2017
Đáp án C
Chia cả tử và mẫu của phân thức cho n3 ( n3 là lũy thừa bậc cao nhất củan trong phân thức), ta được:
u n = 2 n 3 - 3 n 2 + n + 5 n 3 - n 2 + 7 = 2 - 3 n + 1 n 2 + 5 n 3 1 - 1 n + 7 n 3 .
Vì l i m 2 - 3 n + 1 n 2 + 5 n 3 = 2 và l i m 1 - 1 n + 7 n 3 = 1 ≢ 0 nên l i m 2 n 3 - 3 n 2 + n + 5 n 3 - n 2 + 7 = 2 1 = 2 .
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 9 2021
a.
Đề bài sai, ví dụ \(n=1\) lẻ nhưng \(1^2+4.1+8=13\) ko chia hết cho 8
b.
n lẻ \(\Rightarrow n=2k+1\)
\(n^3+3n^2-n-3=n^2\left(n+3\right)-\left(n+3\right)=\left(n^2-1\right)\left(n+3\right)=\left(n-1\right)\left(n+1\right)\left(n+3\right)\)
\(=\left(2k+1-1\right)\left(2k+1+1\right)\left(2k+1+3\right)\)
\(=8k\left(k+1\right)\left(k+2\right)\)
Do \(k\left(k+1\right)\left(k+2\right)\) là tích 3 số tự nhiên liên tiếp nên chia hết cho 6
\(\Rightarrow8k\left(k+1\right)\left(k+2\right)\) chia hết cho 48
8 tháng 1 2024
a: \(n^3-2⋮n-2\)
=>\(n^3-8+6⋮n-2\)
=>\(6⋮n-2\)
=>\(n-2\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
=>\(n\in\left\{3;1;4;0;5;-1;8;-4\right\}\)
b: \(n^3-3n^2-3n-1⋮n^2+n+1\)
=>\(n^3+n^2+n-4n^2-4n-4+3⋮n^2+n+1\)
=>\(3⋮n^2+n+1\)
=>\(n^2+n+1\in\left\{1;-1;3;-3\right\}\)
mà \(n^2+n+1=\left(n+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>=\dfrac{3}{4}\forall n\)
nên \(n^2+n+1\in\left\{1;3\right\}\)
=>\(\left[{}\begin{matrix}n^2+n+1=1\\n^2+n+1=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}n^2+n=0\\n^2+n-2=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}n\left(n+1\right)=0\\\left(n+2\right)\left(n-1\right)=0\end{matrix}\right.\Leftrightarrow n\in\left\{0;-1;-2;1\right\}\)
HT
16 tháng 2 2021
a/ Bạn coi lại đề bài, 3n^2 +n^2 thì bằng 4n^2 luôn chứ ko ai cho đề bài như vậy cả
b/ \(\lim\limits\dfrac{\dfrac{n^3}{n^3}+\dfrac{3n}{n^3}+\dfrac{1}{n^3}}{-\dfrac{n^3}{n^3}+\dfrac{2n}{n^3}}=-1\)
c/ \(=\lim\limits\dfrac{-\dfrac{2n^3}{n^2}+\dfrac{3n}{n^2}+\dfrac{1}{n^2}}{-\dfrac{n^2}{n^2}+\dfrac{n}{n^2}}=\lim\limits\dfrac{-2n}{-1}=+\infty\)
d/ \(=\lim\limits\left[n\left(1+1\right)\right]=+\infty\)
e/ \(\lim\limits\left[2^n\left(\dfrac{2n}{2^n}-3+\dfrac{1}{2^n}\right)\right]=\lim\limits\left(-3.2^n\right)=-\infty\)
f/ \(=\lim\limits\dfrac{4n^2-n-4n^2}{\sqrt{4n^2-n}+2n}=\lim\limits\dfrac{-\dfrac{n}{n}}{\sqrt{\dfrac{4n^2}{n^2}-\dfrac{n}{n^2}}+\dfrac{2n}{n}}=-\dfrac{1}{2+2}=-\dfrac{1}{4}\)
g/ \(=\lim\limits\dfrac{n^2+3n-1-n^2}{\sqrt{n^2+3n-1}+n}+\lim\limits\dfrac{n^3-n^3+n}{\sqrt[3]{\left(n^3-n\right)^2}+n.\sqrt[3]{n^3-n}+n^2}\)
\(=\lim\limits\dfrac{\dfrac{3n}{n}-\dfrac{1}{n}}{\sqrt{\dfrac{n^2}{n^2}+\dfrac{3n}{n^2}-\dfrac{1}{n^2}}+\dfrac{n}{n}}+\lim\limits\dfrac{\dfrac{n}{n^2}}{\dfrac{\sqrt[3]{\left(n^3-n\right)^2}}{n^2}+\dfrac{n\sqrt[3]{n^3-n}}{n^2}+\dfrac{n^2}{n^2}}\)
\(=\dfrac{3}{2}+0=\dfrac{3}{2}\)
PT
1
