Tìm x,y biết: 2x2y-x2-2y-2=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 11 2021
\(1,\\ 12x^6y^3:4x^3y=3x^3y^2\\ \left(x+1\right)\left(x^2-x+1\right)=x^3+1\\ 2x^2y\left(x^2+3xy\right)=3x^4y+6x^3y^2\\ 2,\\ a,=2xy\left(2x+3y-4\right)\\ b,=\left(x-3\right)\left(x+y\right)\\ c,=\left(x-2\right)\left(x+2\right)+y\left(x-2\right)=\left(x+y+2\right)\left(x-2\right)\\ d,=x^2-2x-5x+10=\left(x-2\right)\left(x-5\right)\\ 3,\\ a,\Leftrightarrow x^2-x^2+2x=2\\ \Leftrightarrow2x=2\Leftrightarrow x=1\\ b,\Leftrightarrow\left(x-2\right)\left(x-2+1\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
24 tháng 8 2021
a: Ta có: \(x^2-4y^2-2x-4y\)
\(=\left(x-2y\right)\left(x+2y\right)-2\left(x+2y\right)\)
\(=\left(x+2y\right)\left(x-2y-2\right)\)
c: Ta có: \(x^3+2x^2y-x-2y\)
\(=x^2\left(x+2y\right)-\left(x+2y\right)\)
\(=\left(x+2y\right)\left(x-1\right)\left(x+1\right)\)
d: Ta có: \(3x^2-3y^2-2\cdot\left(x-y\right)^2\)
\(=3\left(x-y\right)\left(x+y\right)-2\cdot\left(x-y\right)^2\)
\(=\left(x-y\right)\left(3x+3y-2x+2y\right)\)
\(=\left(x-y\right)\left(x+5y\right)\)
24 tháng 8 2021
e: Ta có: \(x^3-4x^2-9x+36\)
\(=x^2\left(x-4\right)-9\left(x-4\right)\)
\(=\left(x-4\right)\left(x-3\right)\left(x+3\right)\)
f: Ta có: \(x^2-y^2-2x-2y\)
\(=\left(x-y\right)\left(x+y\right)-2\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y-2\right)\)
MH
14 tháng 10 2023
\(x^2+2y^2-4x+2y+\dfrac{9}{2}=0\)
\(x^2-4x+4+2y^2+2y+\dfrac{1}{2}=0\)
\(\left(x-2\right)^2+2\left(y+\dfrac{1}{2}\right)^2=0\)
Vì \(\left(x-2\right)^2+2\left(y+\dfrac{1}{2}\right)^2\ge0\forall x,y\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-\dfrac{1}{2}\end{matrix}\right.\)
14 tháng 10 2023
\(x^2+2y^2-4x+2y+\dfrac{9}{2}=0\)
=>\(x^2-4x+4+2y^2+2y+\dfrac{1}{2}=0\)
=>\(\left(x-2\right)^2+2\left(y^2+y+\dfrac{1}{4}\right)=0\)
=>\(\left(x-2\right)^2+2\left(y+\dfrac{1}{2}\right)^2=0\)
mà \(\left(x-2\right)^2+2\left(y+\dfrac{1}{2}\right)^2>=0\forall x,y\)
nên \(\left\{{}\begin{matrix}x-2=0\\y+\dfrac{1}{2}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-\dfrac{1}{2}\end{matrix}\right.\)
CM
16 tháng 6 2017
Ta sắp xếp như sau:
Nhóm 1: 3 – 2y; 10x + y; 5(x+y)
Nhóm 2: 4xy2;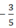 
x2 y3x; 2x2 
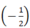y3x; 2x2y; -2y
22 tháng 8 2021
a: Ta có: M+N
\(=-xy^2+3x^2y-x^2y^2+\dfrac{1}{2}x^2y-xy^2+\dfrac{-2}{3}x^2y^2\)
\(=-2xy^2+\dfrac{7}{2}x^2y-\dfrac{5}{3}x^2y^2\)
b: Ta có: N-Q=M
nên \(Q=N-M\)
\(=\dfrac{1}{2}x^2y-xy^2-\dfrac{2}{3}x^2y^2+xy^2-3x^2y+x^2y^2\)
\(=\dfrac{-5}{2}x^2y+\dfrac{1}{3}x^2y^2\)
22 tháng 8 2021
a) \(M+N=-xy^2+3x^2y-x^2y^2+\dfrac{1}{2}x^2y-xy^2-\dfrac{2}{3}x^2y^2=\dfrac{7}{2}x^2y-2xy^2-\dfrac{5}{3}x^2y^2\)b) \(N-Q=M\Rightarrow Q=N-M=\dfrac{1}{2}x^2y-xy^2-\dfrac{2}{3}x^2y^2+xy^2-3x^2y+x^2y^2=-\dfrac{5}{2}x^2y+\dfrac{1}{3}x^2y^2\)c) \(Q=-\dfrac{5}{2}x^2y+\dfrac{1}{3}x^2y^2=-\dfrac{5}{2}.\left(-1\right)^2.\dfrac{1}{2}+\dfrac{1}{3}.\left(-1\right)^2.\left(\dfrac{1}{2}\right)^2=-\dfrac{7}{6}\)
CM
6 tháng 8 2017
Ta có:
A + x 3 y − 2 x 2 y + x − y = 2 y + 3 x + x 2 y ⇔ A = 2 y + 3 x + x 2 y − x 3 y + 2 x 2 y − x + y A = − x 3 y + 3 x 2 y + 2 x + 3 y
Chọn đáp án C
16 tháng 7 2017
1b.=2((x+y)+(x+y)(x-y)+(x-y))=2(x2-y2+x+y+x-y)=2(x2-y2+2x)=2x2-2y2+4x
2a.=4xy+4xy+2y=8xy+2y=2y(4x+1)
b.=(3x)2+2.3x.y+y2-(2z)2=(3x+y)2-(2z)2=(3x+y-2z)(3x+y+2z)
c.=x2-x-7x+7=x(x-1)-7(x-1)=(x-1)(x-7)
30 tháng 9 2018
\(\left(x+y\right)^2+2\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\)
\(=\left(x+y+x-y\right)^2\)
\(=\left(2x\right)^2\)
\(=4x^2\)
hk tốt
^^
28 tháng 10 2021
\(A=x^2\left(x+y\right)+y^2\left(x+y\right)+2xy\left(x+y\right)\\ A=\left(x+y\right)\left(x^2+2xy+y^2\right)=\left(x+y\right)\left(x+y\right)^2\\ A=\left(x+y\right)^3\)
x2(2y-1) - 2y+1-3=0
x2(2y-1)-(2y-1)=3
(x2-1)(2y-1)=3