Cho tam giác ABC đều,cạnh bằng a,đường cao AH.Tính các tích vô hướng sau: a) BA.BC b)HB.BA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 5 2017
Ta có: góc A B → , A C → là góc A ^ nên A B → , A C → = 60 0 .
Do đó A B → . A C → = A B . A C . c o s A B → , A C → = a . a . c o s 60 0 = a 2 2 .
Chọn D.
TM
16 tháng 9 2015
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
AB^2=BH.BC
<=>20^2=BH.(BH + 9)
<=>BH^2 + 9BH-400=0
=> BH=16cm
Mà BC=BH + HC=16 + 9=25cm
AH^2 = BH.HC = 16.9 = 12^2
suy ra AH = 12cm
Vậy diện tích tam giác ABC là:
(AH.BC):2 = (12 . 25) : 2 = 150 cm^2
16 tháng 9 2015
Tam giác ABC vuông tại A , theo HTL
AH^2 = HB.CH
=> 12^2 = 9.CH => CH = 144 : 9 = 16
=> BC = BH + CH = 9 + 16 = 25
=> Sabc = 1/2 BC.AH = 1/2.12.25 = 150 cm^2
LQ
15 tháng 12 2014
1/12 cạnh đáy bằng 1/3 chiều cao
1/12 cạnh đáy bằng 4/12 chiều cao
cạnh đáy gấp 4 lần chiều cao
CĐ XCC/2 = (4X CC) X CC/2 = 72
CC X CC = 36 ; CC= 6
CĐ =DTX2/CC = 72X2/6 = 24
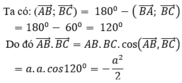
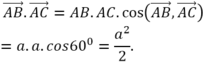
a: \(\overrightarrow{BA}\cdot\overrightarrow{BC}=BA\cdot BC\cdot cos60=\dfrac{1}{2}a^2\)
b: \(\overrightarrow{HB}\cdot\overrightarrow{BA}=\overrightarrow{HB}\left(\overrightarrow{HA}-\overrightarrow{HB}\right)=\overrightarrow{HB}\cdot\overrightarrow{HA}-HB^2=-HB^2=-\dfrac{1}{4}a^2\)