Giúp mình giải bài này với ạ. Bạn An tính bán kính của 1 quả bóng hình cầu như sau: Để quả bóng cách tầm nhìn A một khoảng là AB = 20 cm. Tầm nhìn xa nhất là đoạn AC (C là tiếp điểm của tiếp tuyến vẽ qua A). Biết AC = 40 cm. Em hãy giúp An tính bán kính của quả cầu đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

21 tháng 4 2020
\(\Rightarrow AO\) A M D N B C O
a.Vì AB,AC là tiếp tuyến của (O)
\(\Rightarrow OC\perp AC,OB\perp AB\Rightarrow ON//AB,OM//AC\)
\(\Rightarrow AMON\) là hình bình hành
Mà AB,AC là tiếp tuyến của (O) là phân giác \(\widehat{BAC}\)
\(\Rightarrow AO\)là phân giác \(\widehat{MAN}\)
\(\Rightarrow AMON\) là hình thoi
b ) Gọi AO∩MN=D
Vì AMON là hình thoi \(\Rightarrow AO\perp MN=D\Rightarrow AD=2OD\)
\(\Rightarrow\)Để MN là tiếp tuyến của (O)
\(\Rightarrow OD=R\Rightarrow OA=2OD=2R\)
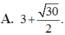
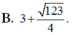
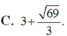
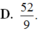

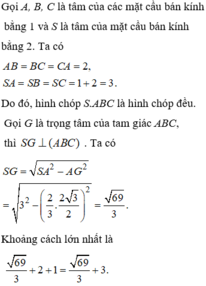



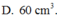

\(BC=\sqrt{40^2-20^2}=20\sqrt{3}\left(cm\right)\)
=>\(R=10\sqrt{3}\left(cm\right)\)