Làm chi tiết với ạ ( Vẽ hình luôn )
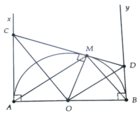
Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By với nửa đường tròn cùng phía đối với AB. Từ điểm M trên nửa đường tròn (M khác A, B) vẽ tiếp tuyên với nửa đường tròn, cắt Ax và By lần lượt tại C và D . Khi đó MC . MD bằng
A.OC\(^2\) B.OM\(^2\) C.OD\(^2\) D.OM

.png)
Chọn B
Cảm ơn ạ