2008*2008*2008*..................*2008
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
B
1
19 tháng 2 2023
https://hoidap247.com/cau-hoi/1164346
Tham khảo vào nhé?
PT
2
H
2
10 tháng 7 2015
ta có Đặt \(A=\frac{2008^{2008}+1}{2008^{2009}+1}\)
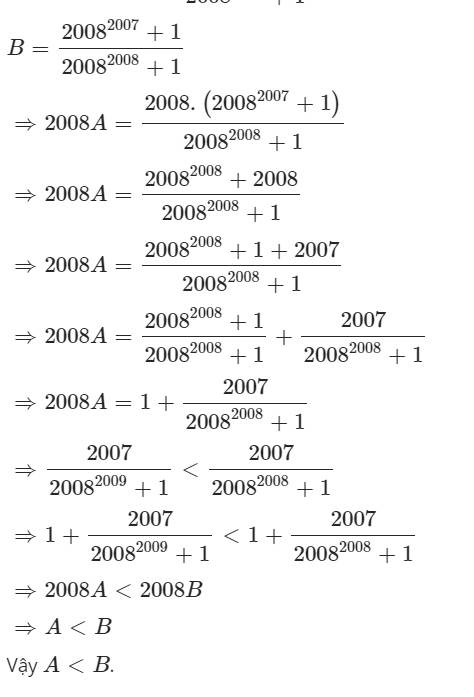
\(B=\frac{2008^{2007}+1}{2008^{2008}+1}\)
Xét A trước ta có
\(2008A=\frac{2008\left(2008^{2008}+1\right)}{2008^{2009}+1}\)\(2008A=\frac{2008^{2009}+2008}{2008^{2009}+1}\)
\(2008A=\frac{2008^{2009}+1+2007}{2008^{2009}+1}\)suy ra \(2008A=1+\frac{2007}{2008^{2009}+1}\)
Xét B ta có
\(2008B=\frac{2008.\left(2008^{2007}+1\right)}{2008^{2008}+1}\)suy ra \(2008B=\frac{2008^{2008}+2008}{2008^{2008}+1}\)
\(2008B=\frac{2008^{2008}+1+2007}{2008^{2008}+1}\)suy ra \(2008B=1+\frac{2007}{2008^{2008}+1}\)
VÌ \(1+\frac{2007}{2008^{2009}+1}
ML
10 tháng 7 2015
Đặt \(a=2008^{2007};\)
\(A=\frac{2008^{2008}+1}{2008^{2009}+1}=\frac{2008a+1}{2008^2.a+1};\text{ }B=\frac{2008^{2007}+1}{2008^{2008}+1}=\frac{a+1}{2008a+1}\)
Quy đồng mẫu ta có:
\(A=\frac{\left(2008a+1\right)\left(2008a+1\right)}{\left(2008^2a+1\right)\left(2008a+1\right)}=\frac{2008^2a^2+2.2008a+1}{\left(2008^2a+1\right)\left(2008a+1\right)}\)
\(B=\frac{\left(a+1\right)\left(2008^2a+1\right)}{\left(2008a+1\right)\left(2008^2a+1\right)}=\frac{2008^2a^2+\left(2008^2+1\right)a+1}{\left(2008a+1\right)\left(2008^2a+1\right)}\)
So sánh ở tử ta thấy \(2.2008
TT
1
27 tháng 9 2015
Bài này hơi dài nên bạn bấn vào đây để xem lời giải Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học toán với OnlineMath
T
21 tháng 9 2023
\(A=\dfrac{2008^{2008}+1}{2008^{2009}+1}\)
\(2008\cdot A=\dfrac{2008^{2009}+2008}{2008^{2009}+1}\)
\(=\dfrac{2008^{2009}+1+2007}{2008^{2009}+1}\)
\(=1+\dfrac{2007}{2008^{2009}+1}\)
\(B=\dfrac{2008^{2007}+1}{2008^{2008}+1}\)
\(2008\cdot B=\dfrac{2008^{2008}+2008}{2008^{2008}+1}\)
\(=\dfrac{2008^{2008}+1+2007}{2008^{2008}+1}\)
\(=1+\dfrac{2007}{2008^{2008}+1}\)
Ta có: \(2008^{2009}+1>2008^{2008}+1\)
\(\Rightarrow\dfrac{1}{2008^{2009}+1}< \dfrac{1}{2008^{2008}+1}\)
\(\Rightarrow\dfrac{2007}{2008^{2009}+1}< \dfrac{2007}{2008^{2008}+1}\)
\(\Rightarrow1+\dfrac{2007}{2008^{2009}+1}< 1+\dfrac{2007}{2008^{2008}+1}\)
hay \(A < B\)
#\(Toru\)
VD
0
HG
0