gpt căn x2-2x+4=x-1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 4 2019
Phần a dễ bạn tự làm nha!!! :))
b, Ta có: \(\Delta^'=\left[-\left(m+1\right)\right]^2-2m=m^2+2m+1-2m=m^2+1>0\forall m\)
=> PT luôn có 2 nghiệm phân biệt
Theo Vi-ét, ta có: \(\hept{\begin{cases}x_1+x_2=2\left(m+1\right)\\x_1x_2=2m\end{cases}}\)
Ta có: \(\sqrt{x_1}+\sqrt{x_2}=\sqrt{2}\)
\(\Leftrightarrow\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=2\)
\(\Leftrightarrow x_1+2\sqrt{x_1x_2}+x_2=2\)
\(\Leftrightarrow x_1+x_2-2+2\sqrt{x_1x_2}=0\)
\(\Leftrightarrow2\left(m+1\right)-2+2\sqrt{2m}=0\)
\(\Leftrightarrow2m+2\sqrt{2m}=0\)
\(\Leftrightarrow m+\sqrt{2m}=0\)
\(\Leftrightarrow\sqrt{m}\left(\sqrt{m}+\sqrt{2}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{m}=0\\\sqrt{m}+\sqrt{2}=0\end{cases}\Leftrightarrow\orbr{\begin{cases}m=0\\\sqrt{m}=-\sqrt{2}\end{cases}}}\)
Vậy: m = 0
=.= hk tốt!!
30 tháng 4 2019
a) Khi m=1 thì pt<=>x2-4x+2=0
Có:\(\Delta\)'=(-2)2-2=2>0=>pt có 2 nghiệm là x1=\(2+\sqrt{2}\)và x2=2-\(\sqrt{2}\)
b)Để pt có nghiệm thì \(\Delta\)'=(m+1)2-2\(\ge\)0<=>m\(\ge\)\(\sqrt{2}\)-1
Theo định lý Viète thì:x1+x2=2(m+1)=\(\sqrt{2}\)<=>\(\frac{\sqrt{2}-2}{2}\)
H
2
19 tháng 9 2020
\(A=\sqrt{x^2-2x+1}+\sqrt{\left(x-4\right)^2}+\sqrt{\left(x-6\right)^2}\)
\(=\sqrt{\left(x-1\right)^2}+\left|x-4\right|+\left|x-6\right|\)
\(=\left|x-1\right|+\left|x-4\right|+\left|x-6\right|\)
\(=\left|x-4\right|+\left(\left|x-1\right|+\left|x-6\right|\right)\)
\(=\left|x-4\right|+\left(\left|x-1\right|+\left|6-x\right|\right)\)
Ta có \(\hept{\begin{cases}\left|x-4\right|\ge0\forall x\\\left|x-1\right|+\left|6-x\right|\ge\left|x-1+6-x\right|=\left|5\right|=5\end{cases}}\)
=> \(\left|x-4\right|+\left(\left|x-1\right|+\left|6-x\right|\right)\ge5\forall x\)
Đẳng thức xảy ra <=> \(\hept{\begin{cases}x-4=0\\\left(x-1\right)\left(6-x\right)\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=4\\1\le x\le6\end{cases}}\Leftrightarrow x=4\)
=> MinA = 5 <=> x = 4
NN
19 tháng 9 2020
Ta có: \(A=\sqrt{x^2-2x+1}+\sqrt{\left(x-4\right)^2}+\sqrt{\left(x-6\right)^2}\)
\(\Rightarrow A=\sqrt{\left(x-1\right)^2}+\sqrt{\left(x-4\right)^2}+\sqrt{\left(x-6\right)^2}\)
\(=\left|x-1\right|+\left|x-4\right|+\left|x-6\right|\)
\(=\left|x-4\right|+\left|x-1\right|+\left|x-6\right|\)
Xét \(\left|x-1\right|+\left|x-6\right|\)ta có:
\(\left|x-1\right|+\left|x-6\right|=\left|x-1\right|+\left|6-x\right|\ge\left|x-1+6-x\right|=\left|5\right|=5\)(1)
Dấu " = " xảy ra \(\Leftrightarrow\left(x-1\right)\left(6-x\right)\ge0\)
TH1: Nếu \(\hept{\begin{cases}x-1< 0\\6-x< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}x< 1\\6< x\end{cases}}\Leftrightarrow\hept{\begin{cases}x< 1\\x>6\end{cases}}\)( vô lý )
TH2: Nếu \(\hept{\begin{cases}x-1\ge0\\6-x\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge1\\6\ge x\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge1\\x\le6\end{cases}}\Leftrightarrow1\le x\le6\)
mà \(\left|x-4\right|\ge0\)(2)
Từ (1) và (2) \(\Rightarrow A\ge5\)
Dấu " = " xảy ra \(\Leftrightarrow\hept{\begin{cases}x-4=0\\1\le x\le6\end{cases}}\Leftrightarrow\hept{\begin{cases}x=4\\1\le x\le6\end{cases}}\Leftrightarrow x=4\)
Vậy \(minA=5\)\(\Leftrightarrow x=4\)
LV
1
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 6 2020
a/ ĐKXĐ: \(1\le x\le5\)
- Với \(4< x\le5\Rightarrow\left\{{}\begin{matrix}VT\ge0\\VP< 0\end{matrix}\right.\) BPT luôn đúng
- Với \(x\le4\) hai vế ko âm, bình phương:
\(-x^2+6x-5>64-32x+4x^2\)
\(\Leftrightarrow5x^2-38x+69< 0\) \(\Rightarrow3< x< \frac{23}{5}\)
Vậy nghiệm của BPT là: \(3< x\le5\)
b/ ĐKXĐ: \(\left[{}\begin{matrix}x\le-5\\x\ge-\frac{4}{3}\end{matrix}\right.\)
- Với \(x< 1\Rightarrow\left\{{}\begin{matrix}VT\ge0\\VP< 0\end{matrix}\right.\) BPT vô nghiệm
- Với \(x\ge1\) hai vế ko âm, bình phương:
\(\left(x+5\right)\left(3x+4\right)< 16\left(x-1\right)^2\)
\(\Leftrightarrow13x^2-51x-4>0\)
\(\Rightarrow x>4\)
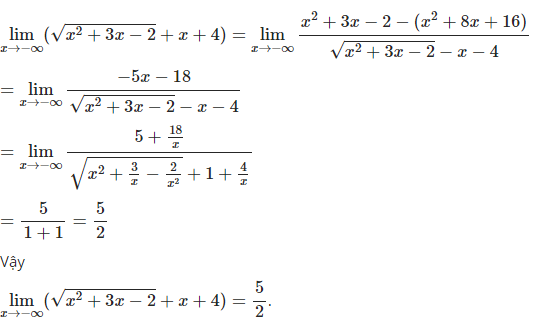
\(\sqrt{x^2-2x+4}=x-1\)
\(\Leftrightarrow\sqrt{\left(x-2\right)^2}=x-1\)
\(\Leftrightarrow x-2=x-1\)
\(\Leftrightarrow x-x=-1+2\)
Giải tới đây thấy vô lý
\(\Rightarrow VNo\)
\(\sqrt{x^2-2x+4}=x-1\)<=> x2-2x+4 =(x-1)2 (Do x2-2x+4 >0)
<=> x2-2x+4 =x2-2x+1 <=> Phương trình vô nghiệm