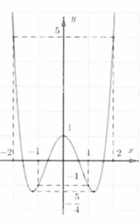
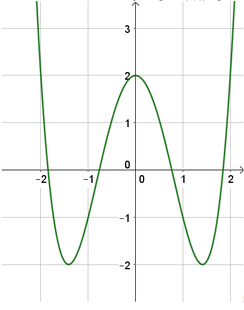
phương trình ax4 + bx2 +c = 0 (a.c < 0) có số nghiệm là...
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 4 2019
Đáp án D
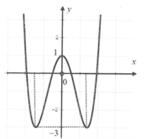
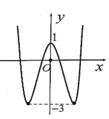
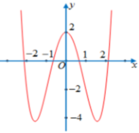
Số nghiệm phương trình (*) là số giao điểm của đồ thị y = f(x) và đường thẳng y = -3
Dựa vào đồ thị thấy có 2 giao điểm suy ra phương trình (*) có 2 nghiệm
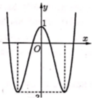
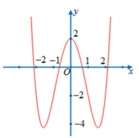
Số nghiệm phương trình (*) là số giao điểm của đồ thị y = f(x) và đường thẳng y = -3
Dựa vào đồ thị thấy có 2 giao điểm suy ra phương trình (*) có 2 nghiệm
CM
30 tháng 8 2017
Chọn đáp án D.
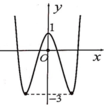
Ta có f(x)+3 = 0 → f(x) = -3 dựa vào đồ thị hàm số suy ra phương trình này có 2 nghiệm phân biệt.
4 tháng 5 2022
Đặt x2=t \(\left(t\ge0\right)\)
=> pt 1 trở thành at2 + bt +c =0 \(\left(2\right)\)
Để pt 1 cso 4 nghiệm phân biệt thì pt 2 phải có 2 nghiệm dương phân biệt
=>\(\left\{{}\begin{matrix}a\ne0\\\Delta>0\\S>0\\P>0\end{matrix}\right.\)
CM
26 tháng 9 2019
Đáp án B
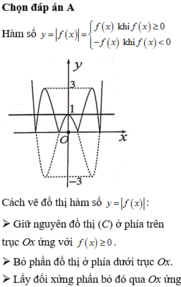
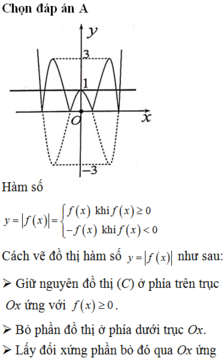
Ta có f x = f x v ớ i x ≥ 0 − f x v ớ i x < 0
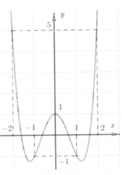
Đồ thị hàm số y = f x được suy ra từ đồ thị hàm số y = f x gồm 2 phần:
- Phần 1: Phần phía bên trên trục hoành.
- Phần 2: Lấy đối xứng với phần phía dưới trục Ox qua trục Ox (bỏ đi phần phía dưới trục hoành).
Khi đó ta được đồ thị hàm số y = f x như sau:
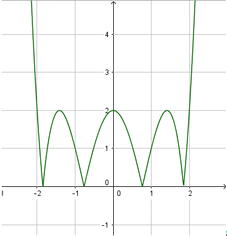
Phương trình f x = log 3 m có 8 nghiệm phân biệt ⇔ 0 < log 3 m < 2 ⇔ 1 < m < 9