Giúp tớ vớii ạa
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
M
8 tháng 9 2023
Tôn Thất Tùng và Trần Đại Nghĩa là hai nhà khoa học nổi tiếng của Việt Nam.
Tôn Thất Tùng là một bác sĩ phẫu thuật, nổi danh trong lĩnh vực nghiên cứu về gan. Ông đã đóng góp rất nhiều cho sự phát triển của y học Việt Nam. Ông đã nghiên cứu và phát triển phương pháp "cắt gan khô" hay còn được gọi là "phương pháp Tôn Thất Tùng". Ông cũng đã nghiên cứu về tác hại của chất độc hóa học điôxin đến con người và môi trường tại Việt Nam. Ông là một trong những nhà khoa học đầu tiên xây dựng phương pháp mổ gan và đã để lại nhiều công trình khoa học quan trọng.
Trần Đại Nghĩa là một kỹ sư quân sự và nhà khoa học lớn của Việt Nam. Ông đã đóng góp rất nhiều cho sự phát triển của ngành công nghiệp quốc phòng Việt Nam. Ông đã nghiên cứu và chế tạo các loại vũ khí như súng và đạn chống tăng Bazooka, súng không giật SKZ cỡ 60mm. Ông cũng đã đặt nền móng cho việc nghiên cứu về tác hại của bom bi và phương pháp điều trị ung thư gan bằng phẫu thuật kết hợp dùng miễn dịch.
Cả hai nhà khoa học này đã có những đóng góp to lớn cho sự phát triển của Việt Nam trong lĩnh vực y học và công nghiệp quốc phòng.
Mik cần gấp lms luôn ạa mng giúp mik vớii
OY
16 tháng 7 2021
Bài 14:
Để số đó nhân với \(\dfrac{7}{25},\dfrac{9}{35},\dfrac{11}{40}\)là tích các số TN thì số đó phải là BCNN(25,35,40)
25=52
35=5.7
40=23.5
BCNN(25,35,40)=52.23.7=1400
Vậy số đó là 1400
16 tháng 7 2021
Bài 16:
a) Ta có: \(A=-\dfrac{9}{5}\)
nên \(\dfrac{3x+9}{17-2x}=\dfrac{-9}{5}\)
\(\Leftrightarrow15x+45=-9\left(17-2x\right)\)
\(\Leftrightarrow15x+45+9\left(17-2x\right)=0\)
\(\Leftrightarrow15x+45+153-18x=0\)
\(\Leftrightarrow-3x=-198\)
hay x=66
b) Thay x=3 vào A, ta được:
\(A=\dfrac{3\cdot3+9}{17-2\cdot3}=\dfrac{18}{17-6}=\dfrac{18}{11}\)
23 tháng 11 2023
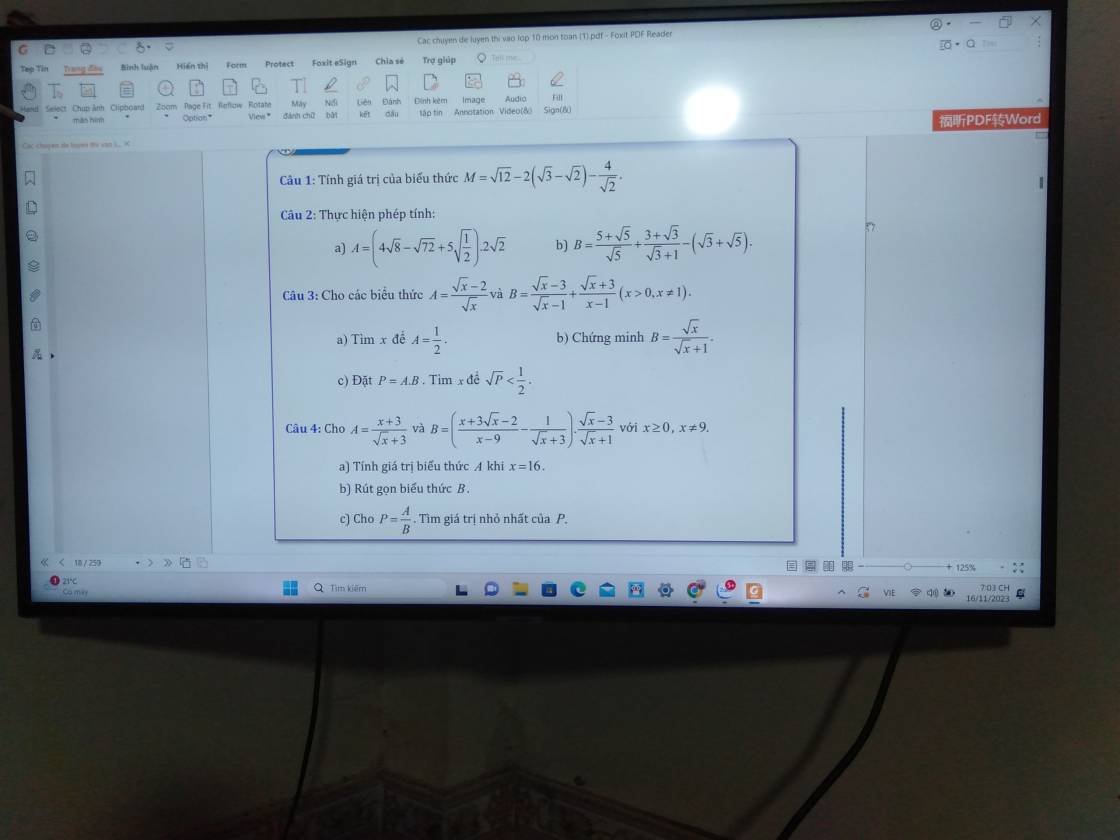
Câu 3:
a: A=1/2
=>\(\dfrac{\sqrt{x}-2}{\sqrt{x}}=\dfrac{1}{2}\)
=>\(2\sqrt{x}-4=\sqrt{x}\)
=>\(2\sqrt{x}-\sqrt{x}=4\)
=>\(\sqrt{x}=4\)
=>x=16(nhận)
b: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}-1}+\dfrac{\sqrt{x}+3}{x-1}\)
\(=\dfrac{\sqrt{x}-3}{\sqrt{x}-1}+\dfrac{\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)+\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-2\sqrt{x}-3+\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
c: \(P=A\cdot B=\dfrac{\sqrt{x}-2}{\sqrt{x}}\cdot\dfrac{\sqrt{x}}{\sqrt{x}+1}=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}\)
\(\sqrt{P}< \dfrac{1}{2}\)
=>\(0< =P< \dfrac{1}{4}\)
=>P>=0 và P<1/4
=>P>=0 và P-1/4<0
=>\(\left\{{}\begin{matrix}\dfrac{\sqrt{x}-2}{\sqrt{x}+1}>=0\\\dfrac{\sqrt{x}-2}{\sqrt{x}+1}-\dfrac{1}{4}< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x}-2>=0\\\dfrac{4\sqrt{x}-8-\sqrt{x}-1}{4\left(\sqrt{x}+1\right)}< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x}>=2\\3\sqrt{x}-9< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}>=2\\\sqrt{x}< 3\end{matrix}\right.\)
=>\(2< =\sqrt{x}< 3\)
=>4<=x<9
KV
8 tháng 11 2023
a) 15 + 4.12 - 3²
=15 + 48 - 9
= 63 - 9
= 54
b) {[(37 + 13) : 5].2 - 45 : 5}.7 - 2022⁰
= [(50 : 5).2 - 9].7 - 1
= (10.2 - 9).7 - 1
= (20 - 9).7 - 1
= 11.7 - 1
= 77 - 1
= 76
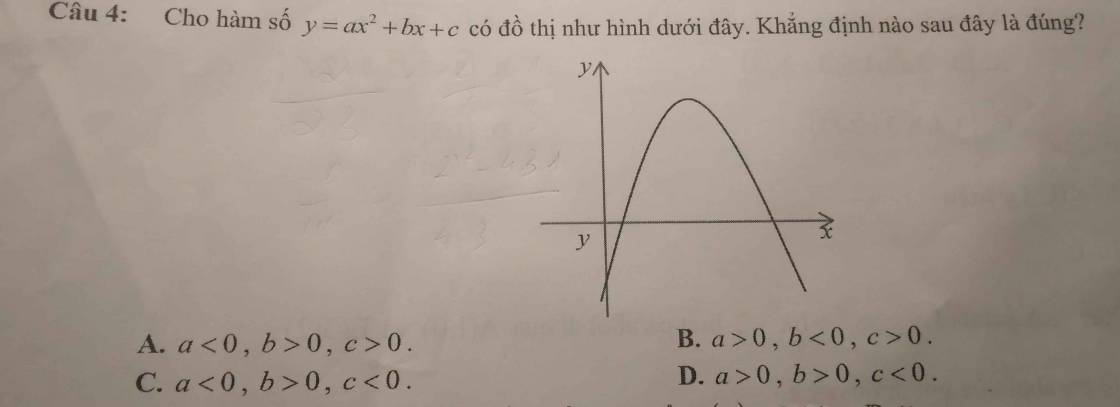
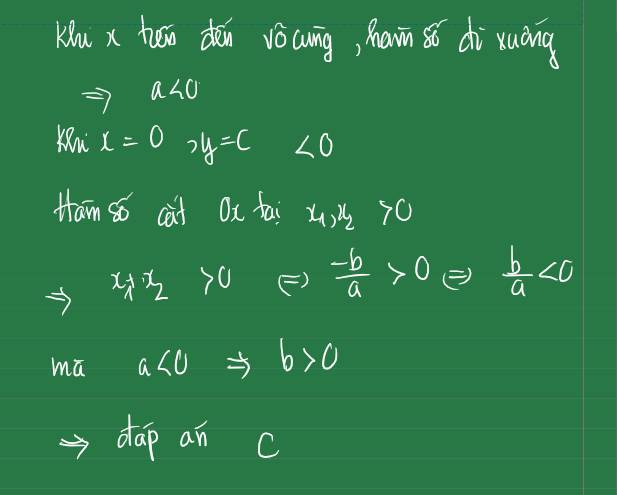
a) \(\left(0,5\right)^{12}:\left(0,5\right)^{10}=\left(0,5\right)^{12-10}=\left(0,5\right)^2\)
b) \(\sqrt{36}=\pm6\)
c)\(\left(0,75\right)^{22}:\left(0,75\right)^{12}=\left(0,75\right)^{22-12}=\left(0,75\right)^{10}\)
d) \(\sqrt{49}=\pm7\)