Để chuẩn bị cho một sự kiện, Ban tổ chức tiến hành rào một khu đất hình chữ nhật để làm bãi giữ xe với một số vật liệu cho trước đủ để làm 180m hàng rào. tại địa điểm được chọn họ tận dụng một một bức tường có sẵn để làm một cạnh của hàng rào. mảnh đất hình chữ nhật được rào như ở trên có diện tích lớn nhất là bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
Gọi x là chiều rộng của vườn hoa (\(x > 0\), tính bằng đơn vị mét)
Theo giả thiết ta có chiều dài là \(15 - x\)
Diện tích của vườn hoa có phương trình như sau \(f\left( x \right) = x\left( {15 - x} \right) = - {x^2} + 15x\)
Ta có bất phương trình thỏa mãn bài toán như sau:\( - {x^2} + 15x \ge 50 \Leftrightarrow - {x^2} + 15x - 50 \ge 0\)
Xét tam thức \(g\left( x \right) = - {x^2} + 15x - 50\) có hai nghiệm phân biệt là \({x_1} = 5;{x_2} = 10\) và \(a = - 1 < 0\) nên \(g\left( x \right) > 0\) khi x thuộc đoạn \(\left[ {5;10} \right]\)
Vậy khi chiều rộng nằm trong đoạn \(\left[ {5;10} \right]\) mét thì diện tích vườn hoa ít nhất là 50 \({m^2}\).
HQ
Hà Quang Minh
Giáo viên
29 tháng 11 2023
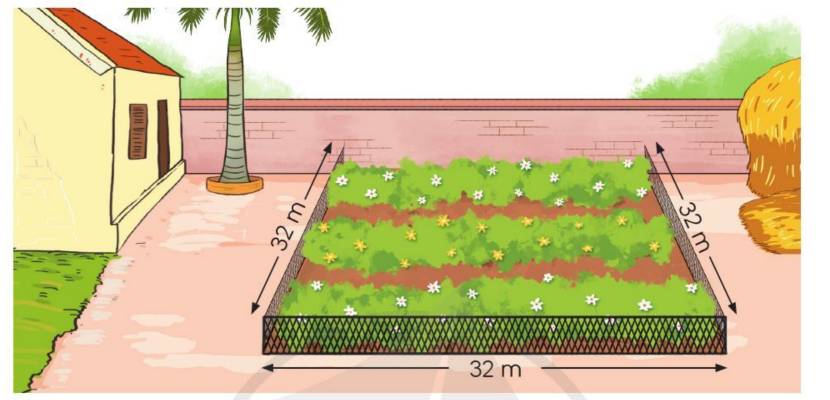
a) Ta có độ dài của hàng rào bằng chu vi hình vuông có cạnh 32 m.
Hàng rào đó dài số mét là
32 × 4 = 128 (m)
Đáp số: 128 m
b) Ta có thể chọn hình 1, hình 3 và hình 4 để có thể ghép thành hình chữ nhật.