Giúp mình với mng ơi, giải chi tiết, rõ ràng, đơn giản để mình dễ hiểu với nhâ 🥹🥹
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ND
1
Những câu hỏi liên quan
ND
1
DT
19 tháng 12 2022
\(n_{N_2}=\dfrac{1792:1000}{22,4}=0,08\left(mol\right)\)
\(5Mg+12HNO_3\rightarrow5Mg\left(NO_3\right)_2+N_2+6H_2O\)
x x \(\dfrac{1}{5}x\)
\(10Al+36HNO_3\rightarrow10Al\left(NO_3\right)_3+3N_2+18H_2O\)
y y \(\dfrac{3}{10}y\)
gọi x và y là số mol của Mg và Al
có hệ: \(\left\{{}\begin{matrix}\dfrac{1}{5}x+\dfrac{3}{10}=0,08\\24+27y=7,8\end{matrix}\right.\)
=> x = 0,1 và y = 0,2
=> \(m_{muôií}=m_{Mg\left(NO_3\right)_2}+m_{Al\left(NO_3\right)_3}=0,1.148+0,2.213=57,4\left(g\right)\)
ND
1
DT
19 tháng 12 2022
\(CuO+CO\underrightarrow{t^o}Cu+CO_2\)
\(MgO+CO->\left(CO.ko.khử,đc\right)\)
\(Fe_2O_3+3CO\underrightarrow{t^o}2Fe+3CO_2\)
\(FeO+CO\underrightarrow{t^o}Fe+CO_2\)
\(n_{CO_2}=\dfrac{4,48}{22,4}=0,2\left(mol\right)\)
Từ các pthh trên thấy: \(n_{CO_2.sinh.ra}=n_{CO.pứ}=0,2\left(mol\right)\left(theo.tỉ.lệ.pthh\right)\)
Áp dụng ĐLBTKL có: \(m_{hh}+m_{CO}=m_{rắn}+mCO_2\)
=> \(m_{rắn}=m_{hh}+m_{CO}-m_{CO_2}=12,5+0,2.28-0,2.44=9,3\left(g\right)\)
HM
1
1 tháng 12 2023
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
=>DA=DE
Xét ΔDAK vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó: ΔDAK=ΔDEC
b: ΔDAK=ΔDEC
=>AK=EC
ΔBAD=ΔBED
=>BA=BE
BA+AK=BK
BE+EC=BC
mà BA=BE và AK=EC
nên BK=BC
d:
Xét ΔBKC có BK=BC
nên ΔBKC cân tại B
ΔBKC cân tại B
mà BH là đường phân giác
nên H là trung điểm của CK
=>HK=HC
17 tháng 8 2023
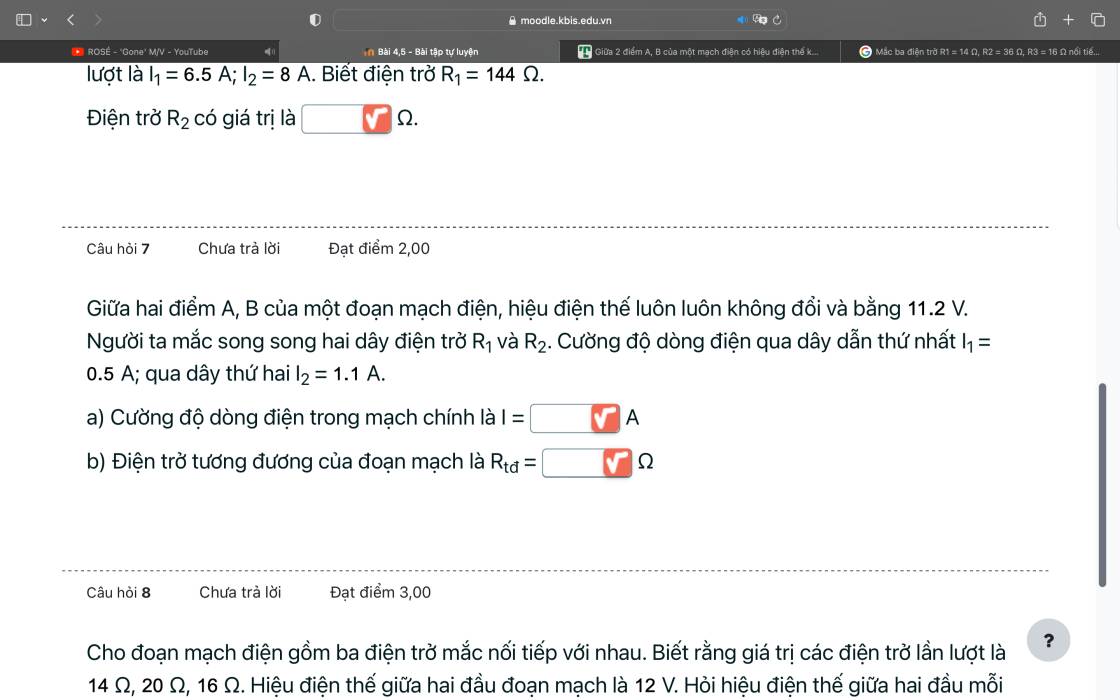
a: R1//R2
=>I=I1+I2=1,6(A)
b: R tđ=11,2/1,6=7(\(\Omega\))
NH
4
AN
1
18 tháng 12 2023
a, Diện tích hình thang cân là
[ 4+(4.3)].5:2=40(cm2)
b, Chu vi hình thang cân là
[4+(4.3)]+(5.2)=26(cm)
Cạnh NP của hình bình hành MNPQ là
(26:2)-4=9(cm)
Đáp số: a,40cm2
b,9cm
\(n_{NO}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\)
\(3R+8HNO_3\rightarrow3R\left(NO_3\right)_2+2NO+4H_2O\)
từ pthh suy ra: \(n_R=\dfrac{3}{2}.n_{NO}=\dfrac{3}{2}.0,1=0,15\left(mol\right)\)
=> \(M_R=\dfrac{9,75}{0,15}=65\)
Vậy tên của R: kẽm (Zn)