Các bạn giải nốt giúp mình hai câu này với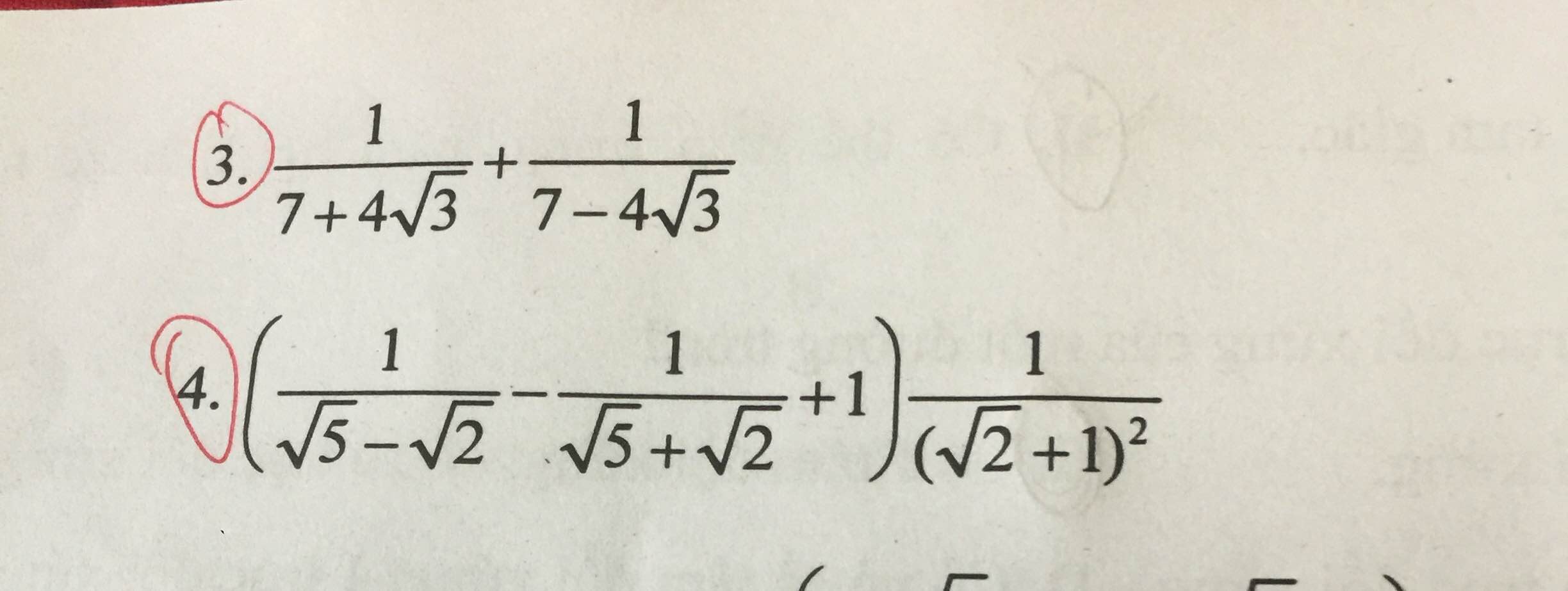
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 11 2021
Áp dụng t/c dtsbn:
\(\dfrac{a+b-c}{c}=\dfrac{a-b+c}{b}=\dfrac{-a+b+c}{a}=\dfrac{a+b-c+a-b+c-a+b+c}{a+b+c}=\dfrac{a+b+c}{a+b+c}=1\)
\(\Rightarrow\left\{{}\begin{matrix}a+b-c=c\\a-b+c=b\\-a+b+c=a\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}a+b=2c\\a+c=2b\\b+c=2a\end{matrix}\right.\)
\(M=\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}=\dfrac{2a.2b.2c}{abc}=8\)
DD
1
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 5 2021
\(f'\left(x\right)=2x^2-x\)
\(f'\left(x\right)\ge0\Leftrightarrow2x^2-x\ge0\)
\(\Leftrightarrow x\left(2x-1\right)\ge0\Rightarrow\left[{}\begin{matrix}x\ge\dfrac{1}{2}\\x\le0\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 5 2021
\(\left\{{}\begin{matrix}BD\perp AC\left(\text{hai đường chéo hình vuông}\right)\\SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
\(\Rightarrow BD\perp SC\)
Mặt khác \(BD\in\left(SBD\right)\Rightarrow\left(SBD\right)\perp\left(SAC\right)\)
b.
Từ A kẻ \(AH\perp SB\)
Ta có: \(\left\{{}\begin{matrix}AD\perp AB\\SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\Rightarrow AD\perp AH\)
\(\Rightarrow AH\) là đường vuông góc chung của AD và SB
\(\Rightarrow AH=d\left(SB;AD\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}=\dfrac{2}{a^2}\Rightarrow AH=\dfrac{a\sqrt{2}}{2}\)
Gọi O là tâm đáy, từ O kẻ \(OK\perp SC\)
Mà \(BD\perp\left(SAC\right)\) theo câu a \(\Rightarrow BD\perp OK\)
\(\Rightarrow OK\) là đường vuông góc chung của SC và BD hay \(OK=d\left(SC;BD\right)\)
\(AC=AB\sqrt{2}=a\sqrt{2}\) ; \(SC=\sqrt{SA^2+AC^2}=a\sqrt{3}\)
\(OK=OC.sin\widehat{SCA}=\dfrac{1}{2}AC.\dfrac{SA}{SC}=\dfrac{a\sqrt{6}}{6}\)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 12 2020
Gọi E là giao điểm của AC và BD thì \(SE=\left(SAC\right)\cap\left(SBD\right)\)
TH
1
G
6 tháng 4 2022
Ta có 1ml = 1cm3
Vậy thể tích của lọ đựng dung dịch đó là 100 cm3
Diện tích trong của đáy lọ là:
Ta có: V = S đáy * h => S đáy = V : h = 100 : 12.5 = 8 (cm2)
TC
2
HT
29 tháng 4 2021
22/ \(\omega A=8\pi\)
\(A^2=x^2+\dfrac{v^2}{\omega^2}\Leftrightarrow A^2=3,2^2+\dfrac{\left(4,8\pi\right)^2}{\omega^2}\)
\(\Leftrightarrow\omega^2A^2=3,2^2\omega^2+23,04\pi^2\Leftrightarrow64\pi^2=3,2^2.\omega^2+23,04\pi^2\Leftrightarrow\omega=2\pi\left(rad/s\right)\)
\(\Rightarrow f=\dfrac{\omega}{2\pi}=\dfrac{2\pi}{2\pi}=1\left(Hz\right)\Rightarrow D.1Hz\)
23/ \(\omega A=20;\omega^2A=80\Rightarrow\left\{{}\begin{matrix}\omega=4\left(rad/s\right)\\A=5cm\end{matrix}\right.\)
\(\Rightarrow v=\omega\sqrt{A^2-x^2}=4.\sqrt{5^2-4^2}=12\left(cm/s\right)\Rightarrow A.12cm/s\)
3: \(=7-4\sqrt{3}+7+4\sqrt{3}=14\)
4: \(=\left(\dfrac{\sqrt{5}+\sqrt{2}-\sqrt{5}+\sqrt{2}+3}{3}\right)\cdot\dfrac{1}{3+2\sqrt{2}}=\dfrac{1}{3}\)