khái niệm giá trị tuyệt đối của X , cách tính giá trị tuyệt đối
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mỗi số thực a là một số phức có phần ảo bằng 0.
Ta có: a ∈ R ⇒ a = a + 0i
Mô đun của số thực a là:
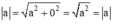
Như vậy với một số thực, khái niệm mô đun và khái niệm giá trị tuyệt đối là đồng nhất.

- Nếu số thực x là một số thực thì môdun x chính là giá trị tuyệt đối của số phức z.
- Nếu số phức z không phải là một số thực thì chỉ có môdun của z, không có khái niệm giá trị tuyệt đối của z.

| x | - | 2 | = 5
=> | x | - 2 = 5
=> | x \ = 7
=> \(\orbr{\begin{cases}x=7\\x=-7\end{cases}}\)
3 | x | = 18
=> | x | = 6
=> \(\orbr{\begin{cases}x=6\\x=-6\end{cases}}\)
2 | x | - 5 = 7
=> | x | = 7 + 5
=> | x | = 12
=> \(\orbr{\begin{cases}x=12\\x=-12\end{cases}}\)
| x | : 3 - 1 = | - 4 |
=> | x | : 3 - 1 = 4
=> | x | : 3 = 5
=> | x | = 15
=> \(\orbr{\begin{cases}x=15\\x=-15\end{cases}}\)

Xin lỗi bài này lớp 6 mình có ôn học sinh giỏi rồi mà quên rồi
ai giúp mik với
Giá trị tuyệt đối của x là 1 số không âm, \(\Rightarrow\left|x\right|=x\) hoặc \(\left|-x\right|\) cũng bằng \(x\)