4x . 4 =16
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
30 tháng 11 2023
Lời giải:
$x^2=4.4.4.4=16.16=(-16)(-16)=16^2=(-16)^2$
$\Rightarrow x=16$ hoặc $x=-16$.
AH
Akai Haruma
Giáo viên
17 tháng 9 2021
Lời giải:
a. ĐKXĐ: $x\in\mathbb{R}$
PT $\Leftrightarrow \sqrt{(x-2)^2}=5$
$\Leftrightarrow |x-2|=5$
$\Leftrightarrow x-2=5$ hoặc $x-2=-5$
$\Leftrightarrow x=7$ hoặc $x=-3$ (đều tm)
b. ĐKXĐ: $x\geq -1$
PT $\Leftrightarrow \sqrt{16}.\sqrt{x+1}-3\sqrt{x+1}+\sqrt{4}.\sqrt{x+1}=16-\sqrt{x+1}$
$\Leftrightarrow 4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}=16-\sqrt{x+1}$
$\Leftrightarrow 4\sqrt{x+1}=16$
$\Leftrightarrow \sqrt{x+1}=4$
$\Leftrightarrow x+1=16$
$\Leftrightarrow x=15$ (tm)
11 tháng 1 2022
\(A=\left(\dfrac{1}{x^2-4x}+\dfrac{2}{16-x^2}+\dfrac{4}{4x+16}\right):\dfrac{1}{4x}\left(x\ne4;x\ne-4;x\ne0\right).\)
\(A=\left(\dfrac{1}{x\left(x-4\right)}+\dfrac{-2}{\left(x+4\right)\left(x-4\right)}+\dfrac{1}{x+4}\right).4x\).
\(A=\dfrac{x+4-2x+x^2-4x}{x\left(x-4\right)\left(x+4\right)}.4x.\)
\(A=\dfrac{x^2-5x+4}{\left(x-4\right)\left(x+4\right)}.4.\)
\(A=\dfrac{\left(x-4\right)\left(x-1\right)}{\left(x-4\right)\left(x+4\right)}.4.\)
\(A=\dfrac{4\left(x-1\right)}{x+4}.\)
4 tháng 1 2018
16+4x^2 / x^4+4x^2
= 4.4+4x^2 / (x^2).(x^2)+4x^2
=4(4+x^2) / x^2(4+x^2)
= 4/x^2
15 tháng 6 2017
(x+4)(x2 -4x-4x+16)
=(x+4)(x2 -8x+16)
=(x-8x)(4+16)(x2)
=-7x.20.x2
=>sap xep x2.(-7x).20
chuc ban hoc tot
H9
HT.Phong (9A5)
CTVHS
24 tháng 9 2023
a) \(\sqrt{x-1}+\sqrt{4x-4}-\sqrt{25x-25}+2=0\) (ĐK: \(x\ge1\))
\(\Leftrightarrow\sqrt{x-1}+\sqrt{4\left(x-1\right)}-\sqrt{25\left(x-1\right)}+2=0\)
\(\Leftrightarrow\sqrt{x-1}+2\sqrt{x-1}-5\sqrt{x-1}+2=0\)
\(\Leftrightarrow-2\sqrt{x-1}=-2\)
\(\Leftrightarrow\sqrt{x-1}=\dfrac{2}{2}\)
\(\Leftrightarrow\sqrt{x-1}=1\)
\(\Leftrightarrow x-1=1\)
\(\Leftrightarrow x=2\left(tm\right)\)
b) \(\sqrt{16x+16}-\sqrt{9x+9}+\sqrt{4x+4}+\sqrt{x+1}=16\) (ĐK: \(x\ge-1\))
\(\Leftrightarrow\sqrt{16\left(x+1\right)}-\sqrt{9\left(x+1\right)}+\sqrt{4\left(x+1\right)}+\sqrt{x+1}=16\)
\(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}=16\)
\(\Leftrightarrow4\sqrt{x+1}=16\)
\(\Leftrightarrow\sqrt{x+1}=4\)
\(\Leftrightarrow x+1=16\)
\(\Leftrightarrow x=15\left(tm\right)\)
TN
6
25 tháng 8 2019
\(4x^4-16-4x^2-16x\)
\(=4x^2\left(x^2-1\right)-16\left(1+x\right)\)
\(=4x^2\left(x+1\right)\left(x-1\right)-16\left(x+1\right)\)
\(=\left(x+1\right)\left[4x^2\left(x-1\right)-16\right]\)
\(=\left(x+1\right)4\left[x^2\left(x-1\right)-4\right]\)
2T
25 tháng 8 2019
Nguyễn Văn Tuấn AnhNs r, không biết thì not làm
\(4x^4-16-4x^2-16x\)
\(=4x^2\left(x^2-1\right)-16\left(x+1\right)\)
\(=4x^2\left(x-1\right)\left(x+1\right)-16\left(x+1\right)\)
\(=\left(x+1\right)\left[4x^2\left(x-1\right)-16\right]\)
\(=4\left(x+1\right)\left[x^2\left(x-1\right)-4\right]\)
\(=4\left(x+1\right)\left[x^3-x^2-4\right]\)
\(=4\left(x+1\right)\left[x^3+x^2+2x-2x^2-2x-4\right]\)
\(=4\left(x+1\right)\left[x\left(x^2+x+2\right)-2\left(x^2+x+2\right)\right]\)
\(=4\left(x+1\right)\left(x-2\right)\left(x^2+x+2\right)\)
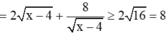
4\(^x\) : 4 = 16
4\(^x\) = 16.4
4\(^x\) = 64
4\(^x\) = 4\(^3\)
=> x=3