| Điểm | Tấn số | Số TBC |
| 4 | 5 | |
| 6 | .... | |
| 7 | 6 | X = 7,55 |
| 9 | .... | |
| 10 | 3 | |
| N = 40 |
Tìm các số còn thiếu trong bảng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ML
3
DR
2
26 tháng 12 2019
Bài giải
Xét hai trường hợp:
TH1: n = 0 thì 20190 + 6 = 1 + 6 = 7 (thỏa mãn)
TH2: n > 0 thì 2019 \(⋮\)3 và 6 \(⋮\)3 (không thỏa mãn)
Vậy n = 0 thì 2019n + 6 là số nguyên tố
24 tháng 8 2021
a. 7, 10, 13,16, 19, 22, 25.
b. 103, 95, 87,79, 71, 63, 55, 47.
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
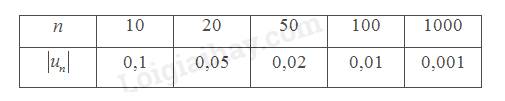
a) \(n = 100 \Leftrightarrow \left| {{u_{100}}} \right| = \left| {\frac{{{{\left( { - 1} \right)}^{100}}}}{{100}}} \right| = \frac{1}{{100}} = 0,01\)
\(n = 1000 \Leftrightarrow \left| {{u_{1000}}} \right| = \left| {\frac{{{{\left( { - 1} \right)}^{1000}}}}{{1000}}} \right| = \frac{1}{{1000}} = 0,001\)
Như vậy ta có thể điền vào bảng như sau:
b) \(\left| {{u_n}} \right| < 0,01 \Leftrightarrow \left| {\frac{{{{\left( { - 1} \right)}^n}}}{n}} \right| < 0,01 \Leftrightarrow \frac{1}{n} < 0,01 \Leftrightarrow n > 100\)
Vậy \(\left| {{u_n}} \right| < 0,01\) khi \(n > 100\).
\(\left| {{u_n}} \right| < 0,001 \Leftrightarrow \left| {\frac{{{{\left( { - 1} \right)}^n}}}{n}} \right| < 0,001 \Leftrightarrow \frac{1}{n} < 0,001 \Leftrightarrow n > 1000\)
Vậy \(\left| {{u_n}} \right| < 0,001\) khi \(n > 1000\).
c) Dựa vào trục số ta thấy, khoảng cách từ điểm \({u_n}\) đến điểm 0 trở nên rất bé khi \(n\) trở nên rất lớn.
ML
1
PT
1
