Giải phương trình: x2+y2+z2=y(x+z)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
1
TT
6 tháng 3 2020
Ta có : \(x^2+y^2\ge2xy\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge\left(x+y\right)^2\)
\(\Leftrightarrow x^2+y^2\ge\frac{\left(x+y\right)^2}{2}\)
Áp dụng vào bài toán có :
\(P\le\frac{x+y}{\frac{\left(x+y\right)^2}{2}}+\frac{y+z}{\frac{\left(y+z\right)^2}{2}}+\frac{z+x}{\frac{\left(z+x\right)^2}{2}}\) \(=\frac{2}{x+y}+\frac{2}{y+z}+\frac{2}{z+x}=\frac{1}{2}\left(\frac{4}{x+y}+\frac{4}{y+z}+\frac{4}{z+x}\right)\)
Áp dụng BĐT Svacxo ta có :
\(\frac{4}{x+y}\le\frac{1}{x}+\frac{1}{y}\), \(\frac{4}{y+z}\le\frac{1}{y}+\frac{1}{z}\), \(\frac{4}{z+x}\le\frac{1}{z}+\frac{1}{x}\)
Do đó : \(P\le\frac{1}{2}\left[2.\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\right]=2016\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=z=\frac{1}{672}\)
P/s : Dấu "=" không chắc lắm :))
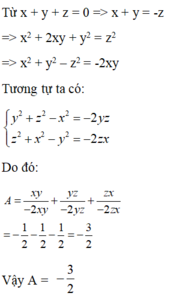
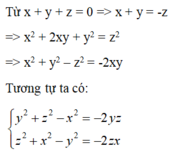
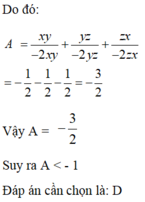
Ta có : \(x^2+y^2+z^2=y\left(x+z\right)\Rightarrow x^2+y^2+z^2-y\left(x+z\right)=0\)
\(\Rightarrow x^2+y^2+z^2-xy-zy=0\Rightarrow\)(nhân 2 vô)\(\Rightarrow2x^2+2y^2+2z^2-2xy-2zy=0\)
\(\Rightarrow\left(x^2-2xy+y^2\right)+\left(y^2-2zy+z^2\right)+z^2=0\)
\(\Rightarrow\left(x-y\right)^2+\left(y-z\right)^2+z^2=0\)\(\Rightarrow x=y=z=0\)
P/S: Bạn trên kia làm sai rồi nhé !
có thể biến đổi trực tiếp a về biến (x-2y)
a=x^2+y^2+xy
=x^2-2xy+y^2+3xy
=x(x-2y)+3xy+y^2
=x(x-2y)+3y(x-2y)+6y^2+y^2
=x+3y+7y^2
=x-2y+5y+7y^2
-------------------ok mất x luôn
=1+5y+7y^2
=7(y^2+5/7.y+1/7)
=7(y^2+2.5/14y+(5/14)^2+1/7-(5/14)^2
=7[(y+5/14)^2+(1/7-5/14)^2]>=7*[1/7-(5/...
=1-5.5.7/7.7.2.2=1-25/28=3/28
đẳng thức khi y=-5/14=> x=5/7+1