Bình dùng đồng hồ đo thời gian để một vật rơi tự do (đơn vị: giây) từ vị trí $A$ đến vị trí $B$ trong 10 lần cho kết quả như sau:
$0,398$ $0,399$ $0,408$ $0,410$ $0,406$ $0,405$ $0,402$ $0,401$ $0,290$ $0,402$ .
Bình nghĩ là giá trị $0,290$ ở lần đo thứ 9 không chính xác. Hãy kiểm tra nghi ngờ của Bình.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có giá trị trung bình:
\(\overline x = \frac{0,398 + 0,399 + 0,408 + 0,410 + 0,406 + 0,405 + 0,402}{7}\)
\( = 0,404\)
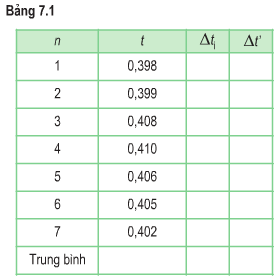
Ta có bảng sau:
Giá trị | Độ lệch | Bình phương độ lệch |
0,398 | 0,006 | \(3,{6.10^{ - 5}}\) |
0,399 | 0,005 | \(2,{5.10^{ - 5}}\) |
0,408 | 0,004 | \(1,{6.10^{ - 5}}\) |
0,410 | 0,006 | \(3,{6.10^{ - 5}}\) |
0,406 | 0,002 | \(0,{4.10^{ - 5}}\) |
0,405 | 0,001 | \(0,{1.10^{ - 5}}\) |
0,402 | 0,002 | \(0,{4.10^{ - 5}}\) |
Tổng | \(12,{2.10^{ - 5}}\) |
Phương sai:
\({s^2} = \frac{{12,{{2.10}^{ - 5}}}}{7} \approx 0,000017\)
Độ lệch chuẩn: \(s = \sqrt {{s^2}} \approx 4,{17.10^{ - 3}}\)
Phép đo có độ chính xác cao.

Để tính kết quả của phép đo thời gian rơi tự do của vật, ta cần lấy trung bình của các kết quả đo và trừ đi sai số của đồng hồ đo.
Trung bình của các kết quả đo là: (0,404 + 0,406 + 0,403) / 3 = 0,4043 s.
Sai số của đồng hồ đo là 0,001 s.
Vậy, kết quả của phép đo thời gian rơi tự do của vật được ghi là 0,4043 - 0,001 = 0,4033 s.

Đáp án B
Ban đầu ta cần phải treo con lắc đơn lên giá tại nơi cần xác định gia tốc trọng trường g. Sau đó dùng thước đo 5 lần chiều dài l của dây treo từ điểm treo tới tâm vật. Tiếp theo kích thích cho vật nhỏ dao động, rồi dùng đồng hồ bấm giây để đo thời gian của một dao động toàn phần để tính được chu kỳ T, lặp lại phép đo 5 lần. Dựa vào công thức trung bình tính giá trị trung bình của chiều dài và chu kỳ sau đó thay vào công thức để tính gia tốc trọng trường trung bình tại ví trí đó.

|
n |
t |
∆ti |
∆t’ |
|
1 |
0,398 |
0,006 |
|
|
2 |
0,399 |
0,005 |
|
|
3 |
0,408 |
0,004 |
|
|
4 |
0,410 |
0,006 |
|
|
5 |
0,406 |
0,002 |
|
|
6 |
0,405 |
0,001 |
|
|
7 |
0,402 |
0,002 |
|
|
Trung bình |
0,404 |
0,004 |
0,001 |

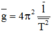
Sắp xếp các giá trị theo thứ tự không giảm:
0,2900,290 0,3980,398 0,3990,399 0,4010,401 0,4020,402 0,4020,402 0,4050,405 0,4060,406 0,4080,408 0,4100,410
Tứ phân vị thứ nhất là 399399, tứ phân vị thứ ba là 406406, do đó \Delta_Q=7ΔQ=7.
Đoạn số liệu không bất thường là [Q_1-1,5 \Delta_QQ1−1,5 ΔQ ; Q_3+1,5 \Delta_QQ3+1,5ΔQ] = [388,5388,5 ; 416,5416,5].
Theo đoạn số liệu không bất thường, ta thấy 0,2090,209 không thuộc đoạn này, do đó kết luận của Bình là hợp lí.