Cho tam giác ABC vuông tại A, đường cao AH. Gọi D và E theo thứ tự là hình chiếu vuông góc của H trên các cạnh AB và AC. Chứng minh: \(S_{ABC}\ge4S_{ADE}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
21 tháng 10 2021
a, BC=BH+HC=8BC=BH+HC=8
Áp dụng HTL:
⎧⎪⎨⎪⎩AB2=BH⋅BC=16AC2=CH⋅BC=48AH2=CH⋅BC=12⇒⎧⎪ ⎪⎨⎪ ⎪⎩AB=4(cm)AC=4√3(cm)AH=2√3(cm){AB2=BH⋅BC=16AC2=CH⋅BC=48AH2=CH⋅BC=12⇒{AB=4(cm)AC=43(cm)AH=23(cm)
b,b, Vì K là trung điểm AC nên AK=12AC=2√3(cm)AK=12AC=23(cm)
Ta có tanˆAKB=ABAK=42√3=2√33≈tan490tanAKB^=ABAK=423=233≈tan490
⇒ˆAKB≈490
CM
8 tháng 10 2019
Vì ADHE là hình chữ nhật nên OD = OH
Suy ra, tam giác ODH cân tại O ⇒ ∠ ODH = ∠ OHD
Mà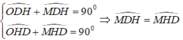 
Xét tam giác MBD có:
∠ (MDB) = ∠ (MBD) (vì cùng phụ với hai góc bằng nhau ∠ (MDH) = ∠ (MHD))
Suy ra, tam giác MBD cân tại M, do đó MD = MB (2)
Từ (1) và (2) suy ra, MB = MH
Vậy M là trung điểm của BH
Tương tự, ta cũng có N là trung điểm của CH.
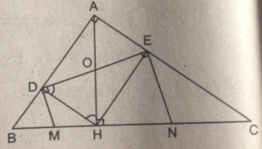
Tứ giác ADHE là hình chữ nhật (có 3 góc vuông) \(\Rightarrow\left\{{}\begin{matrix}AD=EH\\AE=DH\end{matrix}\right.\)
Ta có: \(\dfrac{S_{ABC}}{S_{ADE}}=\dfrac{\dfrac{1}{2}AB.AC}{\dfrac{1}{2}.AD.AE}=\dfrac{AB.AC}{AD.AE}=\dfrac{AB.AC}{DH.EH}=\left(\dfrac{AB}{EH}\right).\left(\dfrac{AC}{DH}\right)\)
Mà \(DH||AC\) (cùng vuông góc AB) \(\Rightarrow\dfrac{AC}{DH}=\dfrac{BC}{BH}\) (Talet)
Tương tự: \(\dfrac{AB}{EH}=\dfrac{BC}{CH}\)
\(\Rightarrow\dfrac{S_{ABC}}{S_{ADE}}=\left(\dfrac{BC}{BH}\right)\left(\dfrac{BC}{CH}\right)=\dfrac{BC^2}{BH.CH}\ge\dfrac{BC^2}{\dfrac{1}{4}\left(BH+CH\right)^2}=\dfrac{4BC^2}{BC^2}=4\) (đpcm)
Dấu "=" xảy ra khi \(BH=CH\) hay tam giác ABC vuông cân tại A