Thu gọn biểu thức A= 2x+7-3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=x.10x+x.7-5x.2x-5x.3+1.2x+1.3+13x\)
\(=10x^2+7x-10x^2-15x+2x+3+13x\)
\(=\left(10x^2-10x^2\right)+\left(7x-15x+2x+13x\right)+3\)
\(=0x^2+7x+3=7x+3\)

\(A= x(10x+7)-(5x-1)(2x+3)+13x\\ = 10x^2+7x-(10x^2+15x-2x-3)+13x\\ = 10x^2+7x-10x^2-15x+2x+3+13x\\ = 7x+3\)
\(A=x.\left(10x+7\right)-\left(5x-1\right).\left(2x+3\right)+13x\)
\(A=10x^2+7x-\left(10x^2+15x-2x-3\right)+13x\)
\(A=10x^2+7x-10x^2-15x+2x+3+13x\)
\(A=\left(10x^2-10x^2\right)+\left(7x-15x+2x+13x\right)+3\)
\(A=7x+3.\)
Chúc bạn học tốt!

5(2x - 3)(2x + 3) - 6(x - 7)2
= 5(2x - 3)(2x + 3) - 6(x2 - 14x + 49)
= 5(4x2 - 9) - 6(x2 - 14x + 49)
= 5.4x2 + 5.(-9) + (-6).x2 + (-6).(-14x) + (-6).49
= 20x2 - 45 - 6x2 + 84x - 294
= 14x2 + 84x - 339


x + 2 x - 3 = x - x + 3 x - 3 = x ( x - 1) + 3( x - 1) = ( x - 1)( x + 3)
a) Với điểu kiện x ≥ 0; x ≠ 1 ta có:
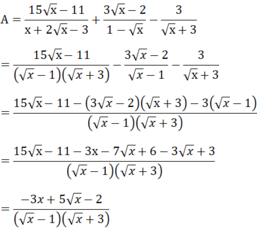
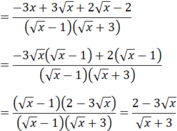

a: =6x-3-|x-5|
Trường hợp 1: x>=5
A=6x-3-x+5=5x+2
Trường hợp 2: x<5
A=6x-3-(5-x)=6x-3+x-5=7x-8
b: Trường hợp 1: x>=-3/2
A=2x+3+x+2=3x+5
Trường hợp 2: x<-3/2
A=-2x-3+x+2=-x-1
`a)3(2x-1)-|x-5|`
`@TH1: x-5 >= 0<=>x >= 5=>|x-5|=x-5`
`=>3(2x-1)-(x-5)=6x-3-x+5=5x+2`
`@TH2: x-5 < 0<=>x < 5=>|x-5|=5-x`
`=>3(2x-1)-(5-x)=6x-3-5+x=7x-8`
____________________________________________________
`b)|2x+3|+x+2`
`@TH1:2x+3 >= 0<=>x >= [-3]/2=>|2x+3|=2x+3`
`=>2x+3+x+2=3x+5`
`@TH2:2x+3 < 0<=>x < [-3]/2 =>|2x+3|=-2x-3`
`=>-2x-3+x+2=-x-1`

\(a,B=4x^2+20x+25-9+x^2+14=5x^2+20x+30\\ b,B=5\left(x^2+4x+4\right)+10\\ B=5\left(x+2\right)^2+10\ge10>0,\forall x\)
Do đó B luôn dương với mọi x
