Cho nửa đường tròn tâm O bán kính R. Hai dây AB // CD có độ dài lần lượt là 25cm, 15cm. Khoảng cách giữa hai dây là 8cm. Tính độ dài bán kính R.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 9 2019
Kẻ OK ⊥ CD ⇒ CK = DK = (1/2).CD
Kẻ OH ⊥ AB ⇒ AH = BH = (1/2).AB
Vì AB // CD nên H, O, K thẳng hàng
Áp dụng định lí Pitago vào tam giác vuông OBH ta có:
O B 2 = B H 2 + O H 2
Suy ra: O H 2 = O B 2 - B H 2 = 25 2 - 20 2 = 225
OH = 15 (cm)
Áp dụng định lí Pitago vào tam giác vuông ODK ta có:
O D 2 = D K 2 + O K 2
Suy ra: O K 2 = O D 2 - D K 2 = 25 2 - 24 2 = 49
OK = 7 (cm)
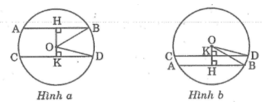
* Trường hợp O nằm giữa hai dây AB và CD (hình a):
HK = OH + OK = 15 + 7 = 22 (cm)
* Trường hợp O nằm ngoài hai dây AB và CD (hình b):
HK = OH – OK = 15 – 7 = 8 (cm)
24 tháng 9 2021
Qua O kẻ đường thẳng vuông góc AB và CD, lần lượt cắt AB và CD tại E và F ⇒ E là trung điểm AB, F là trung điểm CD
AE=12AB=4(cm) ; CF=12CD=3(cm)
Áp dụng định lý pytago cho tam giác vuông OAE
OE=√OA2−AE2=√R2−AE2=3(cm)
Pitago tam giác vuông OCF:
OF=√OC2−CF2=√R2−CF2=4(cm)
⇒EF=OE+OF=7(cm)
chúc bn học tốt !
NW
14 tháng 5 2023
a) Ta có AH là đường cao của tam giác ABC, do đó AB là đường trung trực của đoạn thẳng LH (vì H là trung điểm của BC).
b) Ta có $\angle AED = \angle ACD$ do cùng chắn cung AD trên đường tròn (T). Mà $\angle A = \angle APQ$ vì DE // PQ, nên $\angle AED = \angle APQ$. Tương tự, ta cũng có $\angle ADE = \angle AQP$. Do đó tam giác ADE và APQ đều có hai góc bằng nhau, tức là cân.
c) Ta có $\angle LBD = \angle LCB$ do cùng chắn cung LB trên đường tròn (T). Mà $\angle LCB = \angle LPB$ vì DE // PQ, nên $\angle LBD = \angle LPB$. Tương tự, ta cũng có $\angle LDC = \angle LQC$. Do đó tam giác LBD và LPQ đều có hai góc bằng nhau, tức là đồng dạng. Vậy ta có $\frac{LD}{LP} = \frac{LB}{LQ}$.
Từ đó, có $\frac{LP}{LQ} = \frac{LB}{LD}$. Áp dụng định lý cosin trong tam giác BPQ, ta có:
$PQ^2 = BP^2 + BQ^2 - 2BP \cdot BQ \cdot \cos{\angle PBQ}$
Nhưng ta cũng có:
$BP = LB \cdot \frac{LD}{LP}$
$BQ = L \cdot \frac{LP}{LD}$
Thay vào định lý cosin, ta được:
$PQ^2 = LB^2 + LQ^2 - 2LB \cdot LQ \cdot \frac{LD}{LP} \cdot \frac{LP}{LD} \cdot \cos{\angle PBQ}$
$PQ^2 = LB^2 + LQ^2 - 2LB \cdot LQ \cdot \cos{\angle PBQ}$
Tương tự, áp dụng định lý cosin trong tam giác ADE, ta có:
$DE^2 = AD^2 + AE^2 - 2AD \cdot AE \cdot \cos{\angle AED}$
Nhưng ta cũng có:
$AD = LD \cdot \frac{LB}{LP}$
$AE = LQ \cdot \frac{LD}{LP}$
Thay vào định lý cosin, ta được:
$DE^2 = LD^2 + LQ^2 - 2LD \cdot LQ \cdot \frac{LB}{LP} \cdot \frac{LD}{LP} \cdot \cos{\angle AED}$
$DE^2 = LD^2 + LQ^2 - 2LD \cdot LQ \cdot \cos{\angle AED}$
Nhưng ta cũng có $\angle AED = \angle PBQ$ do tam giác cân ADE và APQ, nên $\cos{\angle AED} = \cos{\angle PBQ}$. Do đó,
$DE^2 + PQ^2 = 2(LB^2 + LQ^2) - 4LB \cdot LQ \cdot \cos{\angle PBQ}$
Nhưng ta cũng có $LB \cdot LQ = LH \cdot LL'$ (với L' là điểm đối xứng của L qua AB), do tam giác HL'B cân tại L'. Thay vào phương trình trên, ta được:
$DE^2 + PQ^2 = 2(LB^2 + LQ^2) - 4LH \cdot LL' \cdot \cos{\angle PBQ}$
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 8 2021
Qua O kẻ đường thẳng vuông góc AB và CD, lần lượt cắt AB và CD tại E và F \(\Rightarrow\) E là trung điểm AB, F là trung điểm CD
\(AE=\dfrac{1}{2}AB=4\left(cm\right)\) ; \(CF=\dfrac{1}{2}CD=3\left(cm\right)\)
Áp dụng định lý Pitago cho tam giác vuông OAE:
\(OE=\sqrt{OA^2-AE^2}=\sqrt{R^2-AE^2}=3\left(cm\right)\)
Pitago tam giác vuông OCF:
\(OF=\sqrt{OC^2-CF^2}=\sqrt{R^2-CF^2}=4\left(cm\right)\)
\(\Rightarrow EF=OE+OF=7\left(cm\right)\)
CM
13 tháng 9 2018
Đáp án B
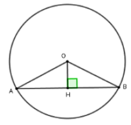
Kẻ OH ⊥ AB tại H suy ra H là trung điểm của AB
Xét tam giác OHB vuông tại H có OH = 3; OB = 5 . Theo định lý Pytago ta có:
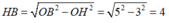
Mà H là trung điểm của AB nên AB = 2HB = 8 cm
Vậy AB = 8 cm
CM
25 tháng 8 2019
Chọn đáp án B.
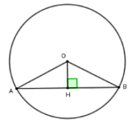
Kẻ OH ⊥ AB tại H suy ra H là trung điểm của AB
Xét tam giác OHB vuông tại H có OH = 3; OB = 5 . Theo định lý Pytago ta có:
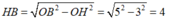
Mà H là trung điểm của AB nên AB = 2HB = 8 cm
Vậy AB = 8 cm
CM
13 tháng 6 2018
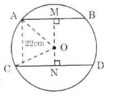
Kẻ OM ⊥ AB, ON ⊥ CD.
Ta thấy M, O, N thẳng hàng. Ta có:
Áp dụng định lí Pitago trong tam giác vuông AMO có:
OM2 = OA2 – AM2 = 252 – 202 = 225
=> OM = √225 = 15cm
=> ON = MN – OM = 22 – 15 = 7 (cm)
Áp dụng định lí Pitago trong tam giác vuông CON có:
CN2 = CO2 – ON2 = 252 – 72 = 576
=> CN = √576 = 24
=> CD = 2CN = 48cm
Tam giác ABC có ˆA>ˆB>ˆCA^>B^>C^ nên suy ra:
BC > AC > AB (cạnh đối diện góc lớn hơn thì lớn hơn)
Ta có AB, BC, AC lần lượt là các dây cung của đường tròn (O)
Mà BC < AC > AB nên suy ra:
OH < OI < OK ( dây lớn hơn gần tâm hơn).