Giúp mình câu 13 14
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 13:
1:
a: \(2x^2+2x=2x\cdot x+2x\cdot1=2x\left(x+1\right)\)
b: \(9x^2-4y^2\)
\(=\left(3x\right)^2-\left(2y\right)^2\)
=(3x-2y)(3x+2y)
2:
\(\dfrac{xy+2x+1}{xy+x+y+1}+\dfrac{yz+2y+1}{yz+y+z+1}+\dfrac{zx+2z+1}{zx+z+x+1}\)
\(=\dfrac{xy+2x+1}{\left(y+1\right)\left(x+1\right)}+\dfrac{yz+2y+1}{\left(z+1\right)\left(y+1\right)}+\dfrac{z\left(x+2\right)+1}{\left(z+1\right)\left(x+1\right)}\)
\(=\dfrac{\left(xy+2x+1\right)\left(z+1\right)+\left(yz+2y+1\right)\left(x+1\right)+\left(xz+2z+1\right)\left(y+1\right)}{\left(x+1\right)\left(y+1\right)\left(z+1\right)}\)
\(=\dfrac{xyz+xy+2xz+2x+z+1+xyz+yz+2xy+2y+x+1+\left(xz+2z+1\right)\left(y+1\right)}{\left(x+1\right)\left(y+1\right)\left(z+1\right)}\)
\(=\dfrac{2xyz+3xy+2xz+3x+z+2+yz+2y+x+xyz+xz+2zy+2z+y+1}{\left(x+1\right)\left(y+1\right)\left(z+1\right)}\)
\(=\dfrac{3xyz+3xy+3xz+3yz+3x+3z+3y+3}{\left(x+1\right)\left(y+1\right)\left(z+1\right)}\)
\(=\dfrac{3\left(xyz+xy+xz+yz+x+z+y+1\right)}{\left(xy+x+y+1\right)\left(z+1\right)}\)
=3
Câu 14:
1:
f(0)=0+5=5
2:
Vì hệ số góc của y=ax+b là -1 nên a=-1
=>y=-x+b
Thay x=1 và y=2 vào y=-x+b, ta được:
b-1=2
=>b=3


Câu 13:
a. Thể tích của viên bi chính là thể tích của nước dâng lên trong bình chia độ
\(V=135-95=40\) (cm3) = \(40.10^{-6}\) (m3)
b. Khối lượng của viên bi là:
\(m=D.V=7800.40.10^{-6}=0,312\) (kg)
c. Trọng lượng của viên bi là:
\(P=10m=10.0,312=3,12\) (N)
Câu 14:
Mặt phẳng nghiêng là một loại máy cơ đơn giản giúp ta kéo vật dễ dàng hơn.
Nếu kéo vật trực tiếp ta cần dùng một lực tối thiểu bằng trọng lượng của vật.
Còn kéo vật bằng mặt phẳng nghiêng ta có thể dùng lực kéo nhỏ hơn trọng lượng của vật, tuy nhiên quãng đường đi sẽ dài hơn.


Câu 13:
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{6^2}{10}=3,6\left(cm\right)\\CH=\dfrac{8^2}{10}=6,4\left(cm\right)\end{matrix}\right.\)
Xét ΔHAB vuông tại H có HM là đường cao
nên \(BM\cdot BA=BH^2\)
=>\(BM\cdot6=3,6^2\)
=>BM=2,16(cm)
Xét ΔHAC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\)
=>\(AN\cdot8=4,8^2\)
=>AN=2,88(cm)
ΔABN vuông tại A
=>\(AB^2+AN^2=BN^2\)
=>\(BN^2=2.88^2+6^2=44,2944\)
=>\(BN=\sqrt{44,2944}=\dfrac{6\sqrt{769}}{25}\left(cm\right)\)
Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
=>AH=MN=4,8(cm)
Xét ΔMBN có \(cosBMN=\dfrac{MB^2+MN^2-NB^2}{2\cdot MB\cdot MN}\)
\(=\dfrac{4,8^2+2,16^2-\dfrac{27684}{625}}{2\cdot4,8\cdot2,16}=\dfrac{-10368}{625}:\dfrac{2592}{125}=-\dfrac{4}{5}\)
=>\(sinBMN=\sqrt{1-\left(-\dfrac{4}{5}\right)^2}=\dfrac{3}{5}\)
Xét ΔBMN có \(\dfrac{NB}{sinBMN}=2R\)
=>\(2R=\dfrac{6\sqrt{769}}{25}:\dfrac{3}{5}=\dfrac{6\sqrt{769}}{25}\cdot\dfrac{5}{3}=\dfrac{2}{5}\sqrt{769}\)
=>\(R=\dfrac{\sqrt{769}}{5}\)
=>Chọn A
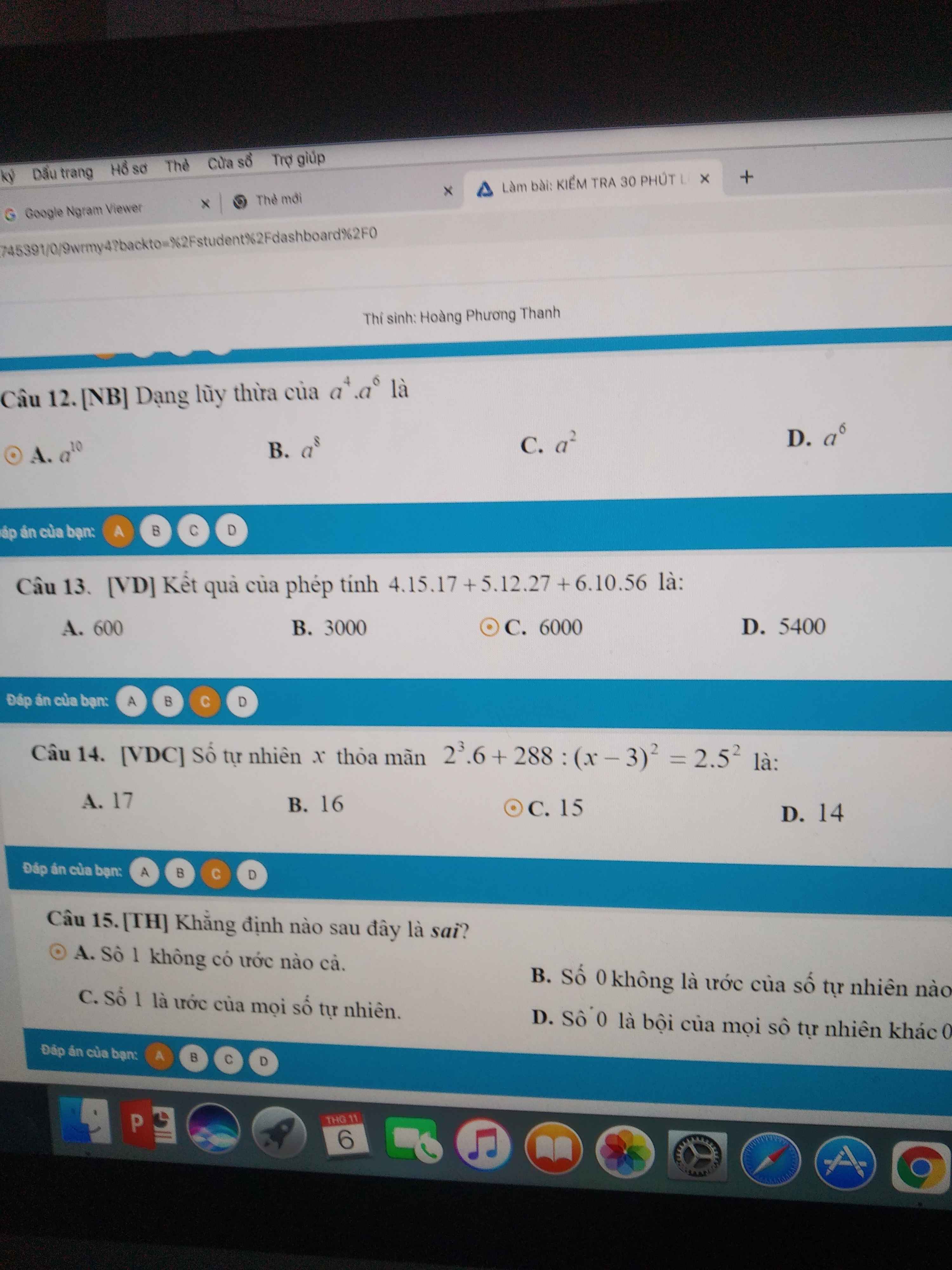



 giải hộ mình câu 13 và câu 14 ạ
giải hộ mình câu 13 và câu 14 ạ

 câu 13, 14, 15 ạ giúp em với
câu 13, 14, 15 ạ giúp em với
13) \(\left\{{}\begin{matrix}n_{CaCO_3}=\dfrac{1}{100}=0,01\left(mol\right)\\n_{Ca\left(HCO_3\right)_2=}n_{CaCO_3\left(thêm\right)}=\dfrac{0,5}{100}=0,005\left(mol\right)\end{matrix}\right.\)
BTNT C: \(n_{CO_2}=n_{CaCO_3}+2n_{Ca\left(HCO_3\right)_2}=0,02\left(mol\right)\)
=> V = 0,02.22,4 = 0,448 (l)
=> B
14) Theo tăng giảm khối lượng:
\(n_{CO_2}=n_{\left(=CO_3\right)}=\dfrac{7,845-7,02}{71-60}=0,075\left(mol\right)\)
=> V = 0,075.22,4 = 1,68 (l)
=> Chọn C