hình chữ nhật ABCD có chiều rộng AD bằng nửa đường chéo AC.Tính số đo góc nhộn tạo bởi hai đường chéo
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 1 2016
Xét tam giác vuông ACD vuông tại A có AD=AC/2 => ACD=30 độ => ADC=60 độ
Gọi giao điểm 2 đường chéo của hcn là O => OA=OD => tam giác AOD cân tại O mà ADC = 60 độ => tam giác AOD đều => AOD=60 độ :)
DN
22 tháng 8 2018
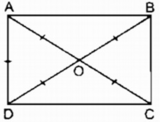
Gọi O là giao điểm của hai đường chéo AC và BD.
AC = BD (tính chất hình chữ nhật)
\(\Rightarrow OA=OD=\dfrac{1}{2}AC\)
\(AD=\dfrac{1}{2}AC\left(gt\right)\)
\(\Rightarrow OA=OD=AD\)
\(\Rightarrow\Delta OAD\) đều
\(\Rightarrow\widehat{AOD}=60^0\)
CM
16 tháng 2 2019
Gọi O là giao điểm của hai đường chéo AC và BD.
Ta có: AC = BD ( tính chất hình chữ nhật) ⇒ OA = OD = 1/2 AC
Lại có: AD = 1/2 AC (gt)
Suy ra: OA = OD = AD
⇒ ∆ OAD đều ⇒ ∠ (AOD ) = 60 0
PT
1
CM
8 tháng 8 2018
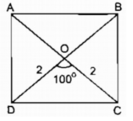
* Cách dựng:
- Dựng ∆ OAB biết OA = OB = 2cm, ∠ (AOB ) = 100 0
- Trên tia đối tia OA dựng điểm C sao cho OC = OA = 2cm
- Trên tia đối tia OB dựng điểm D sao cho OD = OB = 2cm
Nối AD, BC, CD ta có hình chữ nhật ABCD cần dựng
* Chứng minh:
Ta có: OA = OC, OB = OD
Suy ra tứ giác ABCD là hình bình hành.
Vì AC = BD = 4 (cm) nên hình bình hành ABCD là hình chữ nhật.
10 tháng 11 2019
Gọi giao điểm của hai đường chéo là \(O\) .
Theo bài ra thì \(\widehat{AOD}=30^o\)
Theo tính chât hình chữ nhật thì \(OA=OD\) ( cùng bằng nửa độ dài đường chéo )
\(\Rightarrow\Delta OAD\) cân tại O
\(\Rightarrow\widehat{CAD}=\widehat{OAD}=\frac{180^o-\widehat{AOD}}{2}=\frac{180^o-30^o}{2}=75^o\)
Xét tam giác vuông tại D là DAC :
\(\frac{AD}{AC}=cos\widehat{CAD}\Rightarrow AD=cos\widehat{CAD}.AC=cos75^o.4\)
\(\frac{DC}{AC}=sin\widehat{CAD}\Rightarrow DC=ACsin\widehat{CAD}=4sin75^o\)
Do đó diện tích ABCD là :
\(AD.DC=4cos75^o.4sin75^o=4\left(cm^2\right)\)
N
2