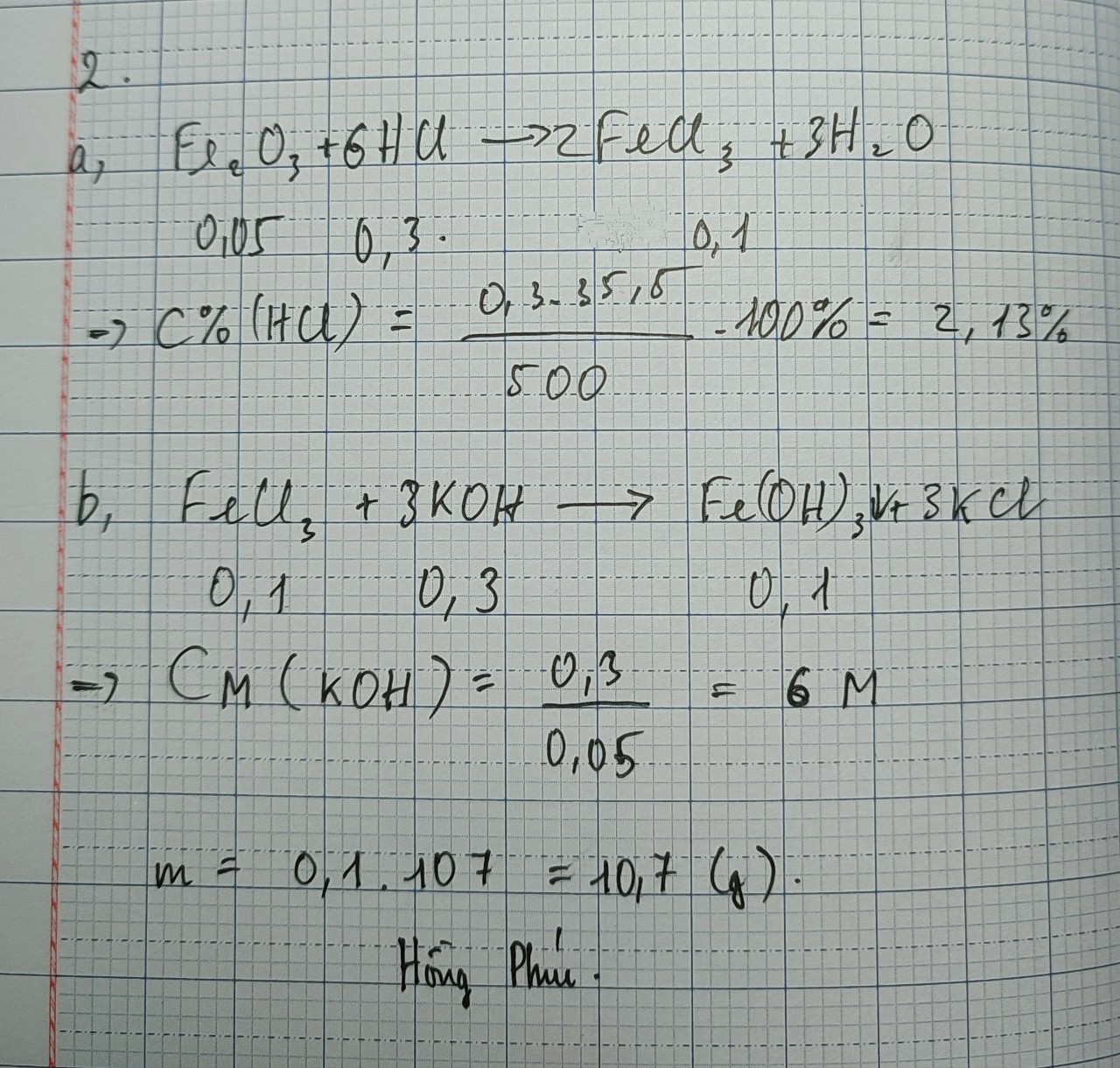Giúp mình câu 2 phần tự luận vs
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
0
DT
25 tháng 4 2022
1.
\(C_{12}H_{22}O_{11}+H_2O\rightarrow C_6H_{12}O_6+C_6H_{12}O_6\)
\(C_6H_{12}O_6\xrightarrow[xt:enzim]{t^o:30-35^o}2C_2H_5OH+2CO_2\)
\(C_2H_5OH+O_2\underrightarrow{xt:men\left(giấm\right)}CH_3COOH+H_2O\)
\(CH_3COOH+C_2H_5OH\underrightarrow{H_2SO_4đặc,t^o}CH_3COOC_2H_5+H_2O\)
25 tháng 4 2022
1.
C12H22O11+H2O→C6H12O6+C6H12O6C12H22O11+H2O→C6H12O6+C6H12O6
C6H12O6to:30−35o−−−−−→xt:enzim2C2H5OH+2CO2C6H12O6→xt:enzimto:30−35o2C2H5OH+2CO2
C2H5OH+O2xt:men(giấm)−−−−−−−−−−−−→CH3COOH+H2OC2H5OH+O2xt:men(giấm)→CH3COOH+H2O
CH3COOH+C2H5OHH2SO4đặc,to−−−−−−−−−−→CH3COOC2H5+H2O
HP
1
YH
1
NT
0
DT
2
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 3 2022
1.
\(\dfrac{3\pi}{2}< a< 2\pi\Rightarrow sina< 0\)
\(\Rightarrow sin\alpha=-\sqrt{1-cos^2a}=-\dfrac{12}{13}\)
\(\Rightarrow tan2a=\dfrac{sin2a}{cos2a}=\dfrac{2sina.cosa}{cos^2a-sin^2a}=\dfrac{2.\left(-\dfrac{12}{13}\right).\left(\dfrac{5}{13}\right)}{\left(\dfrac{5}{13}\right)^2-\left(-\dfrac{12}{13}\right)^2}=...\)
3.
\(P=\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{x}+\dfrac{4}{4y}\ge\dfrac{\left(1+2\right)^2}{x+4y}=\dfrac{9}{6}=\dfrac{3}{2}\)
\(P_{min}=\dfrac{3}{2}\) khi \(\left(x;y\right)=\left(2;1\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 3 2022
4.
Lưu ý: hàm \(sinx\) đồng biến khi \(0< x< 90^0\) và nghịch biến khi \(90^0< x< 180^0\), hàm cos nghịch biến khi \(0< x< 90^0\)
Đường tròn (C) tâm \(I\left(1;1\right)\) bán kính \(R=4\) , \(\overrightarrow{IA}=\left(1;-1\right)\Rightarrow IA=\sqrt{2}\)
Theo công thức diện tích tam giác:
\(S_{IMN}=\dfrac{1}{2}IM.IN.sin\widehat{MIN}=\dfrac{1}{2}R^2.sin\widehat{MIN}=8.sin\widehat{MIN}\)
\(\Rightarrow S_{IMN}\) đạt max khi \(sin\widehat{MIN}\) đạt max
Gọi H là trung điểm MN \(\Rightarrow IH\perp MN\Rightarrow IH\le IA\) theo định lý đường xiên - đường vuông góc
\(\Rightarrow cos\widehat{HIM}=\dfrac{IH}{IM}\le\dfrac{IA}{IM}=\dfrac{\sqrt{2}}{4}\Rightarrow\widehat{HIM}>69^0\)
\(\Rightarrow\widehat{MIN}=2\widehat{HIM}>120^0>90^0\)
\(\Rightarrow sin\widehat{MIN}\) đạt max khi \(\widehat{MIN}\) đạt min
\(\Rightarrow\widehat{HIM}=\dfrac{1}{2}\widehat{MIN}\) đạt min
\(\Rightarrow cos\widehat{HIM}\) đạt max
\(\Rightarrow cos\widehat{HIM}=\dfrac{\sqrt{2}}{4}\Leftrightarrow H\) trùng A
Hay đường thẳng MN vuông góc IA \(\Rightarrow\) MN nhận (1;-1) là 1 vtpt
Phương trình MN: \(1\left(x-2\right)-1\left(y-0\right)=0\Leftrightarrow x-y-2=0\)
