Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Xét ΔABC có
N là trung điểm của AB(gt)
M là trung điểm của AC(gt)
Do đó: NM là đường trung bình của ΔABC
Suy ra: NM//BC và \(NM=\dfrac{BC}{2}\)(1)
Xét ΔGBC có
E là trung điểm của GB
F là trung điểm của GC
Do đó: EF là đường trung bình của ΔGBC
Suy ra: EF//BC và \(EF=\dfrac{BC}{2}\)(2)
Từ (1) và (2) suy ra NM//EF và NM=EF
hay MNEF là hình bình hành
b) Xét ΔABC có
BM là đường trung tuyến ứng với cạnh AC
CN là đường trung tuyến ứng với cạnh AB
BM cắt CN tại G
Do đó: G là trọng tâm của ΔABC
Xét ΔABC có
G là trọng tâm của ΔABC
BM là đường trung tuyến ứng với cạnh AC
Do đó: \(GB=2GM\)
mà GF=2GM
nên GB=GF
hay G là trung điểm của BF
Xét ΔABC có
G là trọng tâm của ΔABC
CN là đường trung tuyến ứng với cạnh AB
Do đó: \(GC=2GN\)
mà GI=2GN
nên GC=GI
hay G là trung điểm của CI
Xét tứ giác BIFC có
G là trung điểm của đường chéo CI(cmt)
G là trung điểm của đường chéo BF(cmt)
Do đó: BIFC là hình bình hành
a) Ta có MN là đường trung bình của ΔABC
⇒ MN // BC và MN = BC/2
Tương tự EF là đường trung bình của ΔBGC nên EF // BC và EF = BC/2
Do đó MN // EF và MN = EF.
Vậy MNEF là hình bình hành (hai cạnh đối vừa song song vừa bằng nhau)
b) Ta có G là trong tâm của ΔABC nên GN = GC/2
Mà GN = JN (gt) ⇒ GJ = GC.
Tương tự ta có GI = GB
Vậy tứ giác BJIC là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).
a) Vì BM là trung tuyến AC
=> M là trung điểm AC (1)
Vì CN là trung tuyến AB
=> N là trung tuyến AB (2)
Từ (1) và (2) => MN là đường trung bình ∆ABC
=> MN //BC , MN = \(\frac{1}{2}BC\)
Vì E là trung điểm GB
F là trung điểm GC
=> FE là đường trung bình ∆GBC
=> FE//BC
=> FE = \(\frac{1}{2}BC\)
=> NM //FE
=> FE= NM
=> NMFE là hình bình hành
a)
ΔABC có: NA= NB; MA = MC
⇒ NM là đường trung bình của ΔABC
⇒ NM // BC; NM = \(\frac{BC}{2}\) (1)
CMTT với ΔGBC, ta được: EF // BC; EF = \(\frac{BC}{2}\) (2)
Từ (1), (2) ⇒ NM // EF; NM = EF
⇒ Tứ giác MNEF là hình bình hành (đpcm)
b)
Hai đường trung tuyến BM và CN cắt nhau ở G
⇒ G là trọng tâm của ΔABC
⇒ CG = 2NG; BG = 2GM
Mà NK = NG ⇒ KG = 2NG
MI = MG ⇒ IG = 2GM
⇒ CG = KG; BG = IG
⇒ Tứ giác BCIK là hình bình hành (đpcm)
\(\frac{BC}{2}\)
a , trong tam giác BGC có EF là đường trung bình => EF // BC ( *)
trong tam giác ABC có MN là đường trung bình => MN // BC ( * * )
từ (*) (**) => EF // MN (1)
nối AG .
trong tam giác ABG có NE là đường trung bình => NE // AG (***)
trong tam giác ACG có MF là đường trung bình => MF // AG (****)
từ (***) (****) => NE // MF (2 )
từ (1) và (2 )
=> MNEF là hình bình hành ( dấu hiệu 1 sgk )
b . đề sai ở chỗ MT = MG phải ko . mình chữa lại là MI = MG
chứng minh
từ câu a , MNEF là hình bình hành => NG = GF và FG = MG
mà : BE = EG = MG = MI => G là trung điểm của BI (1 )
CF = FG = NG = JN => G là trung điểm của JC ( 2)
từ (1 ) và (2) => JC cắt IB tại trung điểm của mỗi đường <=> JIBC là hình bình hành
a, Xét tam giác ABC có G là trọng tâm của tam giác và E;F lần lượt là trung điểm của BG;CG ta có:
\(NG=GF=FC;MG=GE=EB\)(theo tính chất trọng tâm tam giác và trung điểm của 1 cạnh)
\(\Rightarrow MG=EG;NG=FG\)
=> Tứ giác MNEF là hình bình hành(do ME;NF giao nhau tại trung điểm của mỗi cạnh)
b, Theo giả thiết ta có:
\(MI=MG;NJ=NG\)
\(\Rightarrow MI=MG=GE=BE;NJ=NG=GF=CF\)
\(\Rightarrow GI=GB;GJ=GC\)
=> Tứ giác BCIJ là hình bình hành(do BI;CJ giao nhau tại trung điểm của mỗi cạnh)
Vậy........
Chúc bạn học tốt!!!
a: Xét ΔABC có
N là trung điểm của AB
M là trung điểm của AC
DO đó: NM là đường trung bình
=>NM//BC và NM=BC/2(1)
Xét ΔGBC có
E là trung điểm của GB
F là trung điểm của GC
Do đó; EF là đường trung bình
=>EF//BC và EF=BC/2(2)
Từ (1) và (2) suy ra MN//EF và MN=EF
hay MNEF là hình bình hành
b: Xét tứ giác AGBJ có
N là trung điểm của AB
N là trung điểm của GJ
Do đó: AGBJ là hình bình hành
Suy ra: AG//BJ và AG=BJ(3)
Xét tứ giác AGCI có
M là trung điểm của AC
M là trung điểm của GI
Do đó: AGCI là hình bình hành
SUy ra: AG//CI và AG=CI(4)
Từ (3) và (4) suy ra BJ//CI và BJ=CI
hay BJIC là hình bình hành
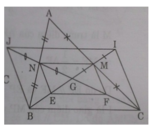
a) xét △abc có MN là dg trung bình → MN//BC
xét △GBC có EF là dg trung bình → EF//BC
⇒ MN // EF(1)
theo tính chất dg trung tuyến thì BG= \(\dfrac{2}{3}\) BM mà BE=EG (gt)
⇒BE = EG = GM
chứng minh tương tự nhu trên ta có NG = GF = FC
cm △NMG = △ EFG (cgc) → NM = EF (2)
từ (1)(2) NMFE là hbh
b) NE là dg trung bình của △GJB → NE//JB
MF là dg tb của △GIC →MF//IC
mà NE//MF ( MNEF là hbh ) ⇒ JB //IC(3)
MN là dg tb của △GIJ → MN//IJ
mà MN //BC (câu a) ⇒ IJ//BC(4)
từ 3&4 ⇒BCIJ là hbh