Bạn Nam đem 20 tờ tiền giấy gồm 2 loại 2000 đồng và 5000 đồng đến siêu thi mua một món quà có giá 78000 đồng và được thối lại 1000 đồng .Hỏi có bao nhieu tờ tiền mỗi loại
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KH
30 tháng 4 2017
p/s: k là nghìn nhé!
Bạn Nam mua món quà giá trị 78000 đồng và được thối lại 1000 đồng => bạn Nam có 79000 đồng.
Ta thấy: Bội số của 5 luôn có tận cùng là 5, bội số của 2 luôn có tận cùng là một số chẵn, mà 79k = 5k (2n + 1) + 4
=> Bạn Nam có 2n + 1 tờ 5k đồng và 2 tờ 2k đồng
=> Số tờ 5 nghìn đồng là: (79k - 4k) : 5 = 15 (tờ)
Vậy bạn Nam có 15 tờ 5 nghìn đồng và 2 tờ 2 nghìn đồng.
kik nha ^v^
5 tháng 2 2017
Tổng số tiền Nam đem là: 78000+10000=88000đ
Gọi số tờ 2000 là x, 5000 là y, ta có hệ pt:
\(\left\{\begin{matrix}x+y=20\\2000x+5000y=88000\end{matrix}\right.\)
giải hệ pt, đc x=4;y=16
=> Số tờ tiền 2000 là 4; số tiền 5000 là 16
giải hệ này dễ thôi: Nhân vế trên cho 2000, rồi trừ cho vế dưới, tìm x,y
2 tháng 7 2023
Gọi số tờ tiền loại 5000 đồng và 10000 đồng Hùng có lần lượt là a,b
Theo đề, ta có:
a+b=16 và 5000a+10000b=120000
=>a=8 và b=8
TH
25 tháng 4
Gọi x là số tờ tiền 5000 đồng và y là số tờ tiền 10000 đồng (x,y€N*;x,y<16)
Vì Hùng đem 16 tờ tiền nên ta có pt: x+y=16(1)
Hùng mua 1 quyển sách trị giá 122000 đồng và được thối lại 3000 đồng nên ta có pt: 5000x+10000y=122000+3000 (2)
Từ (1) và (2) ta có hpt:
X+y=16
5000x+10000y=122000+3000
=> x=7(tmđk)
Y=9 (tmđk)
Vậy Hùng đem theo 7 tờ 5000 đồng và 9 tờ 10000 đồng
10 tháng 7 2021
Tham khảo nha.
Giải thích các bước giải:
Gọi số tờ tiền 2000 đồng là X
2000 × X = 1000 × 3/2 × X
X × X + 3/2 × X = (X + 3/2) × X = (2/2 + 3/2) × X = 7/2 × X
Phương trình để tìm số tờ tiền 2000 đồng.
(125 - 5/2 × X) × 5 + 7/2 × X = 265
625 - 5/2 × 5 × X + 7/2 × X = 265
625 - 25/2 × X + 7/2 × X = 265
625 - 265 = 25/2 × X - 7/2 × X
360 = 25/2 × X - 7/2 × X
360 = (25/2 - 7/2) × X
360 = 9 × X
X = 360 ÷ 9
X = 40
Số tờ tiền 1000 đồng là :
40 ÷ 2/3 = 60 (tờ)
Số tờ tiền 5000 đồng là :
125 - 40 - 60 = 25 (tờ)
Đáp số : Số tờ tiền 1000 đồng là :60 tờ
Số tờ tiền 2000 đồng là :40 tờ
Số tờ tiền 5000 đồng là :25 tờ
CM
2 tháng 8 2017
Gọi x là số tờ giấy bạc loại 5 000 đồng người đó có (0 < x < 15 , x ∈ N).
Vì tổng số tờ 2 000 đồng và 5 000 đồng là 15 tờ nên ta có điều kiện x < 15
và số tờ 2 000 đồng người đó có là: 15 – x (tờ)
⇒ Tổng số tiền người đó có là: 5.x + 2.(15 – x) (nghìn đồng).
Theo bài ra, người đó có số tiền không quá 70 nghìn đồng nên ta có bất phương trình:
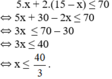
Kết hợp với điều kiện nên x có thể nhận một trong các giá trị {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13}
16 tháng 1 2022
Câu 4:
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=180^0\)
Do đó: MAOB là tứ giác nội tiếp
b: Xét (O) có
ΔABC nội tiếp
AC là đường kính
Do đó: ΔABC vuông tại B
Suy ra:BA\(\perp\)BC
hay OM//CB