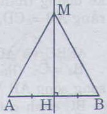
cho đoạn thẳng ab điểm m nằm trên đường trung trực của ab . so sánh độ dài các đoạn thẳng ma và mb
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho đoạn thẳng AB, điểm M nằm trên đường trung trực của AB. So sánh độ dài các đoạn thẳng MA ,và MB.

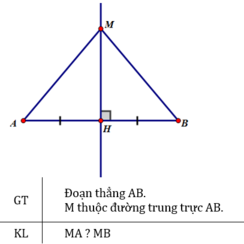
Gọi H là giao điểm của đường trung trực với đoạn AB
⇒ H là trung điểm AB và MH ⊥ AB.
Xét ΔAHM và ΔBHM có:

Nên ΔAHM = ΔBHM
Vậy MA = MB


Hình vẽ: tự vẽ
Đặt AB vuông góc với đường trung trực tại E.
Xét 2 TG AME và BME, ta có:
AE=BE(gt); AEM=BEM=90o; ME; cạnh chung.
=>TG AME=TG BME(c.g.c)
=>MA=MB(2 cạnh tương ứng).

Đặt AB vương góc với đường trung trực tại E
xét 2 TG AME và BME, ta có
AE=BE (gt) AEM=BEM=90 độ ME cạnh chung
suy ra TG AME=TG BME (cgc)
suy ra MA=MB

A B N M
Gọi NM là trung trực AB
=> NA = NB và góc MNA = góc MNB = 90o (Tính chất đường trung trực)
Xét tam giác MNA và tam giác MNB có:
góc MNA = góc MNB (= 90o)
Chung NM
NA = NB (cmt)
=> tam giác MNA = tam giác MNB (c.g.c)
=> MA = MB (2 cạnh tương ứng)

M A B H d
H là trung điểm AB nên AH = BH
d vuông góc với AB \(\Rightarrow\widehat{MHA}=\widehat{MHB}=90^o\)
Xét tam giác AHM và tam giác BHM có :
AH = HB
\(\widehat{MHA}=\widehat{HBM}=90^o\)
MH là cạnh chung
\(\Rightarrow\Delta AHM=\Delta MHB\)
\(\Rightarrow MA=MB\)
Chúc bạn học tốt !!!

xét tam giác amh và tam giác bmh có
ah = hb (gt)
góc ahm = góc bhm (=90 độ)
mh chung
=> tam giác amh = tam giác bmh (c.g.c)